Games202 Hw3 Screen Space Ray Tracing
效果图
由于测试时我电脑的GPU是办公本的核显(GPU AMD Radeon(TM) 530),帧率很低,我就在比较简单的环境(cube1)下比较它们的纯镜面反射差异。
World Space SSR
Efficient GPU SSR
Hierarchical-Z SSR
可以看到Hierarchical-Z SSR的帧率最高,是World Space SSR帧率的4倍,其次是Efficient GPU SSR是World Space SSR帧率的2倍。
作业总览
- 实现直接光照。
- 实现Screen Space Ray Tracing。
- 实现间接光照。
- Bonus 1:实现Mipmap优化的 Screen Space Ray Tracing。
个人扩展:Efficient GPU Screen-Space Ray Tracing
源码
前言
本文重点放在算法本身,源码中相关地方注释很明确,对于框架的理解不再做过多解释。
本次SSR算法总共有三种,分别World Space Ray Marching SSR,Efficient GPU
SSR和Hierarchical-Z
SSR。
实现
World Space Ray Marching SSR
本次作业的基础部分比较简单,算法本身并不复杂,所以这里就附带将SSR Pass的准备工作一并讲一下,这也为后面的算法做好准备。
直接光照
我们先看下渲染方程,这里以SSAO为例讲解一下Visibility怎么处理:

通过上图所说的The RTR Approximation,我们可以得到Visibility拆出后的方程:
\[
\begin{align}
&
L_o(p,w_o)=\int_{\Omega+}L_i(p,w_i)f_r(p,w_i,w_o)V(p,w_i)\cos\theta_i
dw_i \\
& \approx \frac{\rho}{\pi}\cdot
L_i(p)\cdot\pi\cdot\frac{\int_{\Omega+}V(p,w_i)\cos\theta_i dw_i}{\pi}
\tag{1}
\end{align}
\]
但SSAO考虑的是diffuse物体局部范围内不带颜色的全局光照,其积分域在各个方向上都可能有贡献,所以这里要算积分值。
而我们要实现的直接光照是来自平行光,平行光和点光源的一个重要特性:
光源的方向是确定的,也就是说平行光和点光源到着色点只会有一条光线有贡献,其他方向上的贡献为0。那我们也就不用积分了,上述渲染方程直接为:
\[
\begin{align}
L_o(p,w_o)=L_i(p,w_i)f_r(p,w_i,w_o)V(p,w_i)\cos\theta_i
\end{align} \tag{2}
\] 所以代码实现就简单了,如下:
1
2
3
4//直接光照
//L = V * Le * brdf * cos
vec3 L_Normal = GetGBufferNormalWorld(screenUV);
L = EvalDiffuse(screenUV) * EvalDirectionalLight(screenUV) * max(0., dot(L_Normal, wi));V项包含在EvalDirectionalLight函数中。
可以看到Normal等信息是从Gbuffer中获得的,Gbuffer纹理可以理解成是帧缓冲的Color Attachment,我们现在创建一个帧缓冲,并为它提供4个Color Attachment:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class FBO{
constructor(gl, GBufferNum, width, height){
...
function CreateAndBindColorTargetTexture(fbo, attachment, width, height) {
//创建纹理对象并设置其尺寸和参数
var texture = gl.createTexture();
...
gl.bindTexture(gl.TEXTURE_2D, texture);
gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA32F, width, height, 0, gl.RGBA, gl.FLOAT, null);
...
gl.framebufferTexture2D(gl.FRAMEBUFFER, attachment, gl.TEXTURE_2D, texture, 0);
return texture;
};
...
//创建帧缓冲区对象并绑定
var framebuffer = gl.createFramebuffer();
gl.bindFramebuffer(gl.FRAMEBUFFER, framebuffer);
//在JavaScript中,对象是动态的,可以随时添加属性和方法
framebuffer.attachments = [];
framebuffer.textures = []
...
for (var i = 0; i < GBufferNum; i++) {
var attachment = gl.COLOR_ATTACHMENT0 + i;
// var texture = CreateAndBindColorTargetTexture(framebuffer, attachment);
var texture = CreateAndBindColorTargetTexture(framebuffer, attachment, width, height, 0);
framebuffer.attachments.push(attachment);
framebuffer.textures.push(texture);
if(gl.checkFramebufferStatus(gl.FRAMEBUFFER) != gl.FRAMEBUFFER_COMPLETE)
console.log(gl.checkFramebufferStatus(gl.FRAMEBUFFER));
}
// * Tell the WEBGL_draw_buffers extension which FBO attachments are
// being used. (This extension allows for Multiple Render Targets.)
gl.drawBuffers(framebuffer.attachments);
...
return framebuffer;
}
}
camera.fbo = new FBO(gl, 4);
const directionLight = new DirectionalLight(lightRadiance, lightPos, lightDir, lightUp, renderer.gl);ShadowBuffer在创建方向光对象时被创建,而Gbuffer附加在相机对象上,Gbuffer包含的4张纹理如下:
1
2
3
4
5
6
7
8
9
10
11void main(void) {
vec3 kd = texture(uKd, vTextureCoord).rgb;
//albedo
Frag0 = vec4(kd, 1.0);
//depth not linear
Frag1 = vec4(vec3(gl_FragCoord.z), 1.0);
//world space normal(uNt)
Frag2 = vec4(ApplyTangentNormalMap(), 1.0);
//shadow value 0 or 1
Frag3 = vec4(vec3(SimpleShadowMap(vPosWorld.xyz, 1e-4)), 1.0);
}Gbuffer准备好以后,我们就可以得到直接光的效果了:

Screen Space Ray Tracing
SSR就是在屏幕空间上做实时全局光照的一种方法。也就是在屏幕空间做Ray Tracing,而且我们不需要知道三维物体的三角形以及加速结构等,只需要屏幕空间的信息即Gbuffer的内容就可以完成Ray Tracing,也就是得到场景最外的一层壳,然后和这层壳求交。碰到交点后,还要算交点对ShadingPoint的贡献。
具体实现步骤如下图所示:
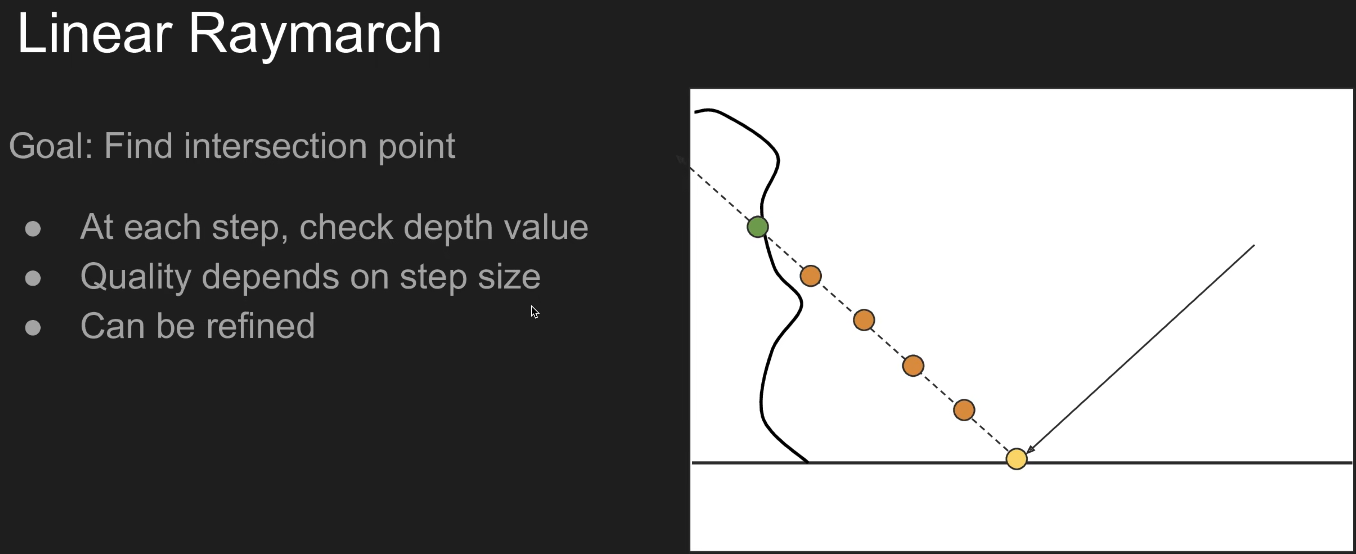
根据BRDF的lobe,生成一根或多根光线,我们假设这里是镜面反射,那就只需要考虑一根反射光线,然后以固定步长沿着反射光线进行步进,每次步进都需要检查步进后光线的深度和场景的深度,直到光线深度大于等于场景深度,就获取该交点处的albedo,然后根据渲染方程进行Shading:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36bool RayMarch(vec3 ori, vec3 dir, out vec3 hitPos) {
float step = 0.02;
const int totalStepTimes = 1000;
int curStepTimes = 0;
vec3 stepDir = normalize(dir) * step;
vec3 curPos = ori;
for(int curStepTimes = 0; curStepTimes < totalStepTimes; curStepTimes++)
{
float curDepth = GetDepth(curPos);
vec2 curScreenUV = GetScreenCoordinate(curPos);
float gBufferDepth = GetGBufferDepth(curScreenUV);
if(curDepth - gBufferDepth > 0.0001){
hitPos = curPos;
return true;
}
//o + t * d
curPos += stepDir;
}
return false;
}
// test Screen Space Ray Tracing
vec3 EvalReflect(vec3 wi, vec3 wo, vec2 uv) {
vec3 worldNormal = GetGBufferNormalWorld(uv);
vec3 relfectDir = normalize(reflect(-wo, worldNormal));
vec3 hitPos;
if(RayMarch(vPosWorld.xyz, relfectDir, hitPos)){
vec2 screenUV = GetScreenCoordinate(hitPos);
return GetGBufferDiffuse(screenUV);
}
else{
return vec3(0.0);
}
}
//test
L = EvalReflect(wi,wo,screenUV);SSR是否能正常工作,没有考虑渲染方程,所以这里EvalReflect只是简单的返回交点处的Albedo。一切正常的话就会得到下面的图片:
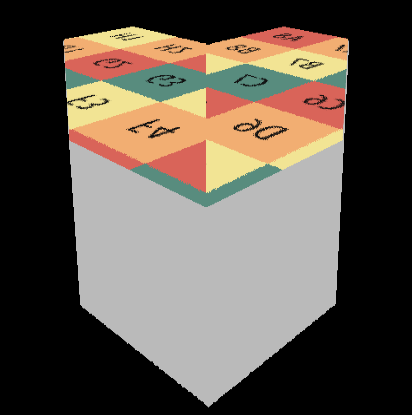
间接光照
有了上面的基础,间接光照就是直接算渲染方程的积分值。
在算积分之前,我们需要知道采样方向以及它的Pdf,然后用蒙特卡洛积分来计算。这里对于兰伯特材质直接使用Cos-weighted采样。其过程如下:
使用Cos-weighted采样,意味着Pdf和Cos项成正比,即pdf(w)=c*cosθ,则:
\[
\begin{align}
& \int_{\Omega^+}pdf(w)dw=1 \\
& \int_{\Omega^+}c\cdot\cos\theta dw=1 \\
& \int_{0}^{2\pi}\int_{0}^{\pi/2}c\cdot\cos\theta\sin\theta d\theta
d\phi \\
& =\int_{0}^{2\pi}\int_{0}^{\pi/2}c\cdot\sin\theta d\sin\theta d\phi
\\
& =\int_{0}^{2\pi}c\cdot \frac{\sin^2\theta}{2}\vert_{0}^{\pi/2}
d\phi \\
& =c\cdot\pi \tag{3}
\end{align}
\]
则c=1/π,pdf=cosθ/π。采样方向还是用逆变换采样的方式来获取:
分别求其边缘概率密度函数:
\[
\begin{align}
& p(\theta)=\int_{0}^{2\pi}\frac{\cos\theta\sin\theta}{\pi}d\phi \\
& =2\cos\theta\sin\theta \\
& p(\phi)=\int_{0}^{\pi/2}\frac{\cos\theta\sin\theta}{\pi}d\theta \\
& =\frac{\sin^2\theta}{2\pi}\vert_{0}^{\pi/2} \\
& =\frac{1}{2\pi} \tag{4}
\end{align}
\] 分别求其累积分布函数:
\[
\begin{align}
& P(\theta)=\int_{0}^{\theta}2\cos\theta\sin\theta d\theta \\
& =\sin^2\theta \\
& =1-\cos^2\theta \\
& P(\phi)=\int_{0}^{\phi}\frac{1}{2\pi}d\phi \\
& =\frac{\phi}{2\pi} \tag{5}
\end{align}
\] 均匀的从U[0,1]中取出两个随机数\(X_{1}\)和\(X_{2}\),则我们要的采样θ和φ为:
\[
\begin{align}
\theta=\arccos(\sqrt{1-X_1}) \\
\phi=2\pi X_2 \tag{6}
\end{align}
\] 则采样方向vec(x,y,z)为:
\[
\begin{align}
& x=\sin\theta\cos\phi=\sqrt{X_1}\cos(2\pi X_2) \\
& y=\sin\theta\sin\phi=\sqrt{X_1}\sin(2\pi X_2) \\
& z=\cos\theta=\sqrt{1-X_1} \tag{7}
\end{align}
\] 对应代码如下:
1
2
3
4
5
6
7
8
9vec3 SampleHemisphereCos(inout float s, out float pdf) {
vec2 uv = Rand2(s);
float z = sqrt(1.0 - uv.x);
float phi = uv.y * TWO_PI;
float sinTheta = sqrt(uv.x);
vec3 dir = vec3(sinTheta * cos(phi), sinTheta * sin(phi), z);
pdf = z * INV_PI;
return dir;
}Pdf,用蒙特卡洛公式计算积分值:
\[
\begin{align}
L_o(p,w_o)\approx\frac{1}{N}\sum_{k=1}^{N}\frac{L_{i}(p,w_{i})f_{r}(p,w_{i},w_{o})\cos(\theta_{i})}{p(w_{i},w_{o})}
\tag{8}
\end{align}
\] 代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26//直接光照
//L = V * Le * brdf * cos
vec3 L_Normal = GetGBufferNormalWorld(screenUV);
L = EvalDiffuse(screenUV) * EvalDirectionalLight(screenUV) * max(0., dot(L_Normal, wi));
//间接光
vec3 L_ind = vec3(0.0);
for(int i = 0; i < SAMPLE_NUM; i++){
float pdf;
vec3 localDir = SampleHemisphereCos(s, pdf);
vec3 L_ind_Normal = GetGBufferNormalWorld(screenUV);
vec3 b1, b2;
LocalBasis(L_ind_Normal, b1, b2);
vec3 dir = normalize(mat3(b1, b2, L_ind_Normal) * localDir);
//world space pos
vec3 hitPos;
if(RayMarch(worldPos, dir, hitPos)){
vec2 hitScreenUV = GetScreenCoordinate(hitPos);
//castRay = V * Le * brdf * cos.
vec3 hitNormal = GetGBufferNormalWorld(hitScreenUV);
vec3 castRay = EvalDiffuse(hitScreenUV) * EvalDirectionalLight(hitScreenUV) * max(0., dot(hitNormal, wi));
//L_ind += castRay * brdf * cos / pdf
L_ind += castRay * EvalDiffuse(screenUV) * max(0., dot(L_ind_Normal, dir)) / pdf;
}
}
L_ind /= float(SAMPLE_NUM);
L = L + L_ind;World Space Ray Marching SSR的效果如下:

要想得到不错的效果需要用实时光追降噪或者提高采样数量,读者可以自己学完实时光追降噪后应用于此,我电脑不行就不折腾了。下面是洞穴的效果:

Efficient GPU SSR
Digital Differential Analyzer
Efficient GPU SSR的核心思想是DDA(Digital
Differential Analyzer),该算法是用数值方法求解微分方程。
我们简单回顾一下DDA思想:
给定理想直线的起点坐标为\(P_0(x_0,y_0)\)终点坐标为\(P_1(x_1,y_1)\),用斜截式表示的直线方程为:
\[
\begin{align}
y=kx+b \tag{9}
\end{align}
\] 其中直线的斜率为\(k=\frac{\Delta
y}{\Delta x}\),\(\Delta
x=x_1-x_0\)为水平方向位移,\(\Delta
y=y_1-y_0\)为垂直方向位移,b为y轴上的截距。
在DDA算法中,常根据\(\Delta x\)和\(\Delta
y\)的大小来确定绘图的主位移方向,在主位移方向上执行的是\(\pm 1\),选定\(\Delta\)较大方向为主方向使得斜率k满足\(0\leq
k\leq1\)(若δy大于δx则交换它们的值):
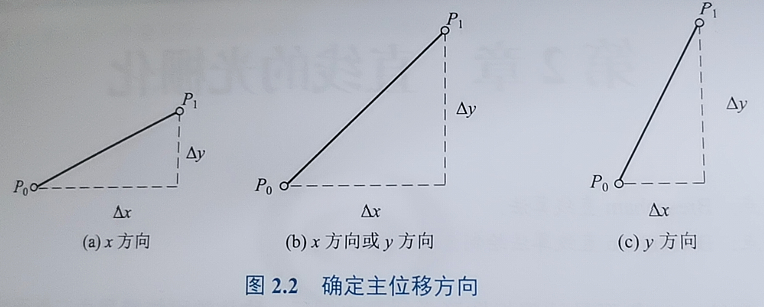
确定主方向后,上面9式的微分表示为: \[
\begin{align}
\frac{\text{d}y}{\text{d}x}=\frac{\Delta y}{\Delta x}=\frac{\delta
y}{\delta x}=k \tag{10}
\end{align}
\] 其有限差分近似解为:
\[
\begin{equation}
\left\lbrace
\begin{aligned}
& x_{i+1}=x_i+\delta x=x_i+1 \\
& y_{i+1}=y_i+\delta y=y_i+k\delta x=y_i+k
\end{aligned}
\right.
\end{equation}
\] \(\Delta
x\)每次步进一个像素,根据上一次的点位\((x_i,y_i)\)就可以确定当前的点\((x_{i+1},y_{i+1})\)。最后将求得的点位进行\(\text{int}(y_{i+1}+0.5)\)取整即可得到对应的像素。
最后得到的效果如图:
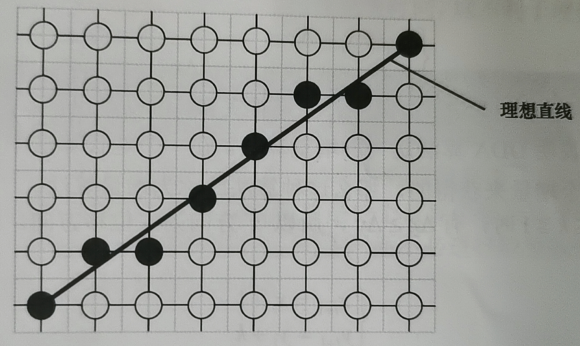
An Efficient GPU DDA Solution
对于3D空间中大多数反射光线,3D线性采样并不等同于2D线性采样,如下图所示。因此,即使步长已经取的很小,一次步进可能也会跳过屏幕上的多个像素点(这里是误差的主要来源),而且会出现多次步进都是对同一个像素点采样的情况(低效的主要原因)。
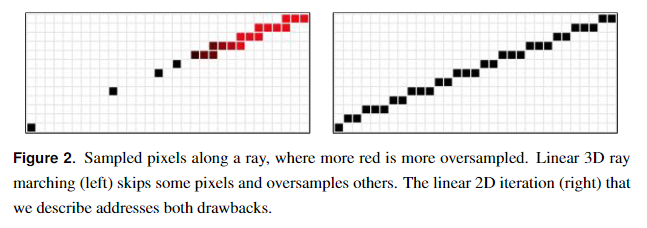
右边的效果是我们这一节的主要内容。
重点是RayMarching函数,该函数的输入是ViewSpace下的反射方向以及它的起点,为了方便这里还是以纯镜面反射为例,全局光照参考World Space Ray Marching SSR可以实现。获取这两个参数的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20vec3 EvalReflect(vec3 wo,vec2 screenUV) {
vec3 normalWS = GetGBufferNormalWorld(screenUV);
vec3 reflectDir = normalize(reflect(-wo,normalWS));
vec3 rayOriginWS = vPosWorld.xyz;
vec3 rayEndWS = rayOriginWS + reflectDir * 1.0;
vec3 rayOriginVS = projectToViewSpace(rayOriginWS);
vec3 rayEndVS = projectToViewSpace(rayEndWS);
vec3 reflectDirVS = normalize(rayEndVS - rayOriginVS);
Ray ray;
ray.Origin = rayOriginVS;
ray.Direction = reflectDirVS;
Result result = RayMarching(ray);
if(result.IsHit){
return GetGBufferDiffuse(result.UV / vec2(windowWidth,windowHeight)).xyz;
}
else{
return vec3(0.0);
}
}3D线段光栅化与2D线段光栅化非常相似。光栅化可以很容易地沿迭代方向对任何属性进行线性插值。如果属性处于齐次空间,则结果将线性插值3D空间中对应的属性值。具体来说,设点Q为射线上的一个3D点,H = M·(Q,1)为其左乘透视投影矩阵M的齐次透视投影。属性k = 1/(H·(0,0,0,1))和Q·k可以在2D中线性插值。因此,如果把该点和齐次w的倒数看作是沿2D线的函数,那么∂(Q·k) / ∂x,∂k / ∂x,∂(Q·k) / ∂y,和∂k / ∂y在屏幕空间中都是常数。
其中∂(Q·k) / ∂x,∂k / ∂x,∂(Q·k) / ∂y,和∂k / ∂y是函数Q·k的偏微分表示。
∂(Q·k) / ∂x表示函数 Q·k 对 x 的偏微分,即改变 x 时 Q·k
的变化情况。
∂k / ∂x表示函数 k 对 x 的偏微分,即改变 x 时 k
的变化情况。
∂(Q·k) / ∂y表示函数 Q·k 对 y 的偏微分,即改变 y 时 Q·k
的变化情况。
∂k / ∂y表示函数 k 对 y 的偏微分,即改变 y 时 k
的变化情况。
在任意2D线段上的点\(Q(x,y)\),其对应的三维点为\(Q'\):
\[
\begin{align}
& Q'(x,y)=\frac{(Q·k)(x,y)}{k(x,y)} \\
& Q'(z)=\frac{(Q·k)(z)}{k(z)} \tag{11}
\end{align}
\]
有了3D深度信息后,我们就可以和Gbuffer中的深度信息进行比对了。在此之前我们需要知道∂(Q·k) / ∂x,∂k / ∂x偏微分的数值表示,而Gbuffer中的深度信息读取需要另一个偏微分∂y / ∂x。
在上面有提到在线性情况下,偏微分的值都是常数,则:
\[
\begin{align}
& \frac{∂(Q·k)}{∂x}=\frac{\Delta(Q·k)}{\Delta x}=\frac{\delta
(Q·k)}{\delta x}=dQ \\
& \frac{∂k}{∂x}=\frac{\Delta k}{\Delta x}=dK \\
& \frac{∂y}{∂x}=\frac{\Delta y}{\Delta x}=dP \tag{12}
\end{align}
\]
为了方便这里常数分别取名为dQ,dK,dP。有了这些信息后,我们想要的属性就可以通过增量来算得了,假设Q为(Q·k)的别名,则\(Q_{i+1}.z=Q_i.z+δQ_i.z=Q_i.z+\delta x\cdot
dQ\),其中δx==1,相应的\(k_{i+1}=k_i+dK\)。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81struct Result
{
bool IsHit;
vec2 UV;
...
};
bool Query(float depth, vec2 uv)
{
float depth1 = -LinearizeDepth(texelFetch(uGDepth,ivec2(uv),0).r);
return depth < depth1;
}
//DDA,数值方法求解微分方程的算法
Result RayMarching(Ray ray)
{
Result result;
//endPos 不能超出近平面,否则反射出的颜色是错误的。超过的话origin沿dir到近平面的距离 = origin到近平面的最短距离 / cosθ,cosθ = dir.z / r;
float rayLength = ((ray.Origin.z + ray.Direction.z * maxDistance) > -uZBufferParams.x) ?
(-uZBufferParams.x - ray.Origin.z) / ray.Direction.z : maxDistance;
vec3 V0 = ray.Origin;
vec3 V1 = ray.Origin + ray.Direction * rayLength;
//将viewSpace下的origin和endPos转到ClipSpace
vec4 H0 = projectToClipSpace(V0);
vec4 H1 = projectToClipSpace(V1);
float k0 = 1.0 / H0.w;
float k1 = 1.0 / H1.w;
vec3 Q0 = V0 * k0;
vec3 Q1 = V1 * k1;
// NDC-space
vec2 P0 = H0.xy * k0;
vec2 P1 = H1.xy * k1;
vec2 Size = vec2(windowWidth,windowHeight);
//Screen Space
P0 = (P0 + 1.0) / 2.0 * Size;
P1 = (P1 + 1.0) / 2.0 * Size;
vec2 Delta = P1 - P0;
//是否重新排序,我们只处理Delta较大情况
bool Permute = false;
if (abs(Delta.x) < abs(Delta.y)) {
Permute = true;
Delta = Delta.yx; P0 = P0.yx; P1 = P1.yx;
}
float StepDir = sign(Delta.x);
float Invdx = StepDir / Delta.x;
//偏微分的数值表示法
vec3 dQ = (Q1 - Q0) * Invdx;
float dk = (k1 - k0) * Invdx;
vec2 dP = vec2(StepDir, Delta.y * Invdx);
float stride = 2.0;//可调
dP *= stride; dQ *= stride; dk *= stride;
float jitter = 1.0;//可调
P0 += dP * jitter; Q0 += dQ * jitter; k0 += dk * jitter;
float Step = 0.0;
float MaxStep = 1000.0;
float EndX = P1.x * StepDir;
float k = k0;
vec3 Q = Q0;
vec2 P = P0;
for(;((P.x * StepDir) <= EndX) &&
Step < MaxStep;
Step+=1.0,P += dP, Q.z += dQ.z, k += dk)
{
result.UV = Permute ? P.yx : P;
float depth;
//At any 2D point (x,y), the corresponding 3D point is Q‘(x,y)=(Q·k)(x,y) / k(x,y),Q’(z)=(Q·k)(z) / k(z)
depth = Q.z / k;
if(result.UV.x > windowWidth || result.UV.x < 0.0 || result.UV.y > windowHeight || result.UV.y < 0.0)
break;
result.IsHit = Query(depth, result.UV);
if (result.IsHit)
break;
}
return result;
}rayLength光线的长度不能超过近平面,否则会出错,光线长度超出了近平面的范围则用下面等式进行约束:
origin沿dir到近平面的距离 = origin到近平面的最短距离 / cosθ,cosθ = dir.z / r(cartesian
to spherical in tangent space)。
如果一切顺利,将会得到下面效果图:

Hierarchical-Z SSR
Hi-Z是为了优化线性步进的算法,因为步长是固定的,但是大部分时间都浪费在了没有碰撞的空间中。
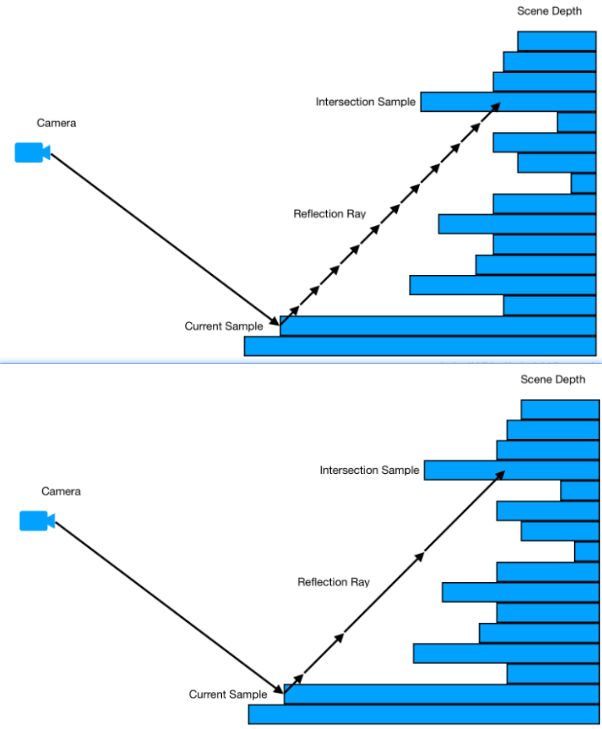
而Hi-Z会根据试探步来判断下一次步长的距离,如果试探步没有与场景相交,那下一次步进的距离就更大,这样求得的交点所使用的步进次数更少,在保证准确率的情况下,效率也得到了极大的提升!
Hi-Z方法创建了一个Depth Mipmap加速结构,称为Hi-Z buffer。该结构本质上是场景深度的四叉树,其中每个四叉树层级中的每个单元格都被设置为上一层级中4个单元格的最小值(或最大值,取决于z轴方向)。
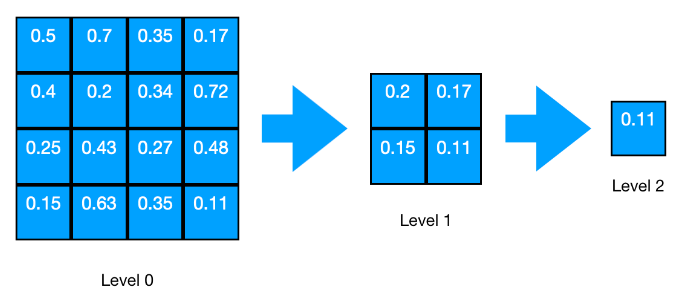
值得注意的是,如果行或列不是偶数,采样需要额外多加一列或一行,如果都是奇数,那么还要额外多考虑一个右上角的像素,如图:
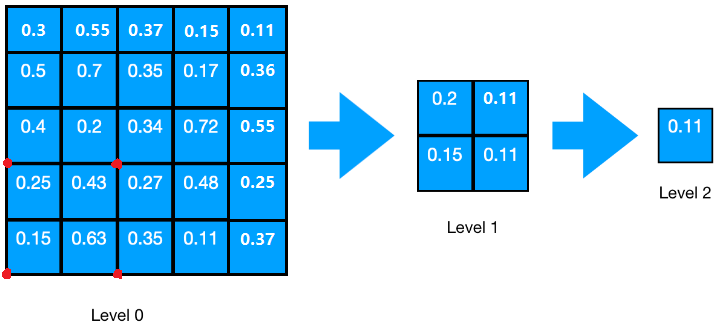
这部分代码比较散就不列出来了,理解了这个过程,实现就不难了。
Depth Mipmap可以用另一个Pass来看每一层效果,效果如下:

越黑表示越近,纯白色就是深度为1.0的情况无限远。
有了Depth Mipmap,我们还需要屏幕空间的起点和方向。获取这些数据的过程和上一节差不多,代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30vec3 EvalReflect(vec3 wo,vec2 screenUV) {
//从世界坐标中恢复Ts中的原点和反射方向
vec3 normalWS = GetGBufferNormalWorld(screenUV);
vec3 reflectDir = normalize(reflect(-wo,normalWS));
vec3 rayOriginWS = vPosWorld.xyz;
vec3 rayEndWS = rayOriginWS + reflectDir * 1.0;
vec3 rayOriginVS = projectToViewSpace(rayOriginWS);
vec3 rayEndVS = projectToViewSpace(rayEndWS);
vec4 rayOriginCS = projectToClipSpace(rayOriginVS);
vec4 rayEndCS = projectToClipSpace(rayEndVS);
rayOriginCS = rayOriginCS.xyzw / rayOriginCS.w;
rayEndCS = rayEndCS.xyzw / rayEndCS.w;
vec3 rayOriginTS = (vec3(rayOriginCS) + 1.0) * 0.5;
vec3 rayEndTS = (vec3(rayEndCS) + 1.0) * 0.5;
vec3 reflectDirTS = normalize(rayEndTS - rayOriginTS);
float outMaxDistance = reflectDirTS.x >= 0.0 ? (1.0 - rayOriginTS.x) / reflectDirTS.x : -rayOriginTS.x / reflectDirTS.x;
outMaxDistance = min(outMaxDistance, reflectDirTS.y < 0.0 ? (-rayOriginTS.y / reflectDirTS.y) : ( (1.0-rayOriginTS.y) / reflectDirTS.y));
outMaxDistance = min(outMaxDistance, reflectDirTS.z < 0.0 ? (-rayOriginTS.z / reflectDirTS.z) : ((1.0-rayOriginTS.z)/reflectDirTS.z));
SSRay ray;
ray.rayPosInTS = rayOriginTS;
ray.rayDirInTS = reflectDirTS;
ray.maxDistance = outMaxDistance;
vec3 hitPos;
vec3 reflectedColor = vec3(0.);
if(FindIntersection_HiZ(ray, hitPos)) {
reflectedColor = GetGBufferDiffuse(hitPos.xy);
}
return reflectedColor;
}outMaxDistance是防止反射终点超出屏幕而浪费性能。
接下来就是重头戏,FindIntersection_HiZ函数的实现。
该函数核心地方就是试探步如何确定下次步进的距离,先说下这里试探步是怎么处理的,我先把相关代码贴出来,以便参考和解释。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18vec3 intersectDepthPlane(in vec3 o, in vec3 d, float t){
return o + d * t;
}
...
vec3 start = ss_ray.rayPosInTS;
vec3 rayDir = ss_ray.rayDirInTS;
float maxTraceDistance = ss_ray.maxDistance;
vec3 ray = start;
float minZ = ray.z;
float maxZ = ray.z + rayDir.z * maxTraceDistance;
float deltaZ = (maxZ - minZ);
vec3 o = ray;
vec3 d = rayDir * maxTraceDistance;
...
//步进起点所在单元格的GbufferDepth
float cell_minZ = getMinimumDepthPlane((oldCellIdx + 0.5) / cellCount, level);
//试探步:步进起点的深度小于GbufferDepth,则步进到ray.z >= gbufferDepth的地方,这可能会导致新的tmpRay.xy超过1.0,所以这里只是试探步,实际步进是用intersectCellBoundary这个函数完成。
vec3 tmpRay = (cell_minZ > ray.z) ? intersectDepthPlane(o, d, (cell_minZ - minZ) / deltaZ) : ray;ray为例,我们假设这里ray已经向rayDir步进了一小段距离以防止自相交。我们先看下intersectDepthPlane这个函数,以公式o+t*d来确定步进后的点,需要注意的是,这里的d指代的是非单位向量,即:光线终点 - 光线起点。而t则是一个归一化的系数在[0,1]之间,有了t这个系数,这样我们就可以精确的得到起点沿光线步进后的点。
下面用图例的形式进一步解释试探步:
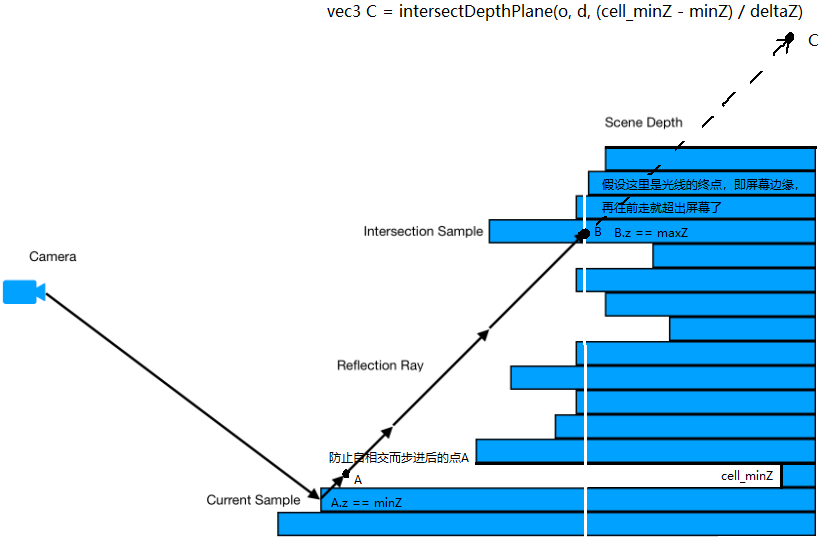
可以看到如果起点A要试探地走一步,这一步有可能会直接跨出屏幕(假设白色线条代表屏幕的位置),或者跨过了多个像素,从而错过中间可能会相交的点。我们从试探步中得到的信息就是,它这一步是否跨过了起点A所在的像素,如果跨过了起点A所在的单元格(像素),那我们就用另一个函数使得起点A步进到下一个单元格。需要注意的是这里的单元格和Depth Mipmap层级挂钩的,层级越大,一个单元格的步长就越大。
下面我们解释一下如何让起点A步进到下一个单元格,还是先看下相关代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58bool FindIntersection_HiZ(
in SSRay ss_ray,
out vec3 intersection
) {
vec3 start = ss_ray.rayPosInTS;
vec3 rayDir = ss_ray.rayDirInTS;
float maxTraceDistance = ss_ray.maxDistance;
vec2 crossStep = vec2(rayDir.x >= 0.0 ? 1.0 : -1.0, rayDir.y >= 0.0 ? 1.0 : -1.0);
vec2 crossOffset = crossStep / vec2(windowWidth,windowHeight) / 128.;
//假设reflectDir不与屏幕的宽高平行,如果是向前步进一个单元格的距离,boundary = (rayCell + crossStep )/ cell_count + crossOffset,其中crossOffset > 0.
//如果是向后步进一个单元格的距离,boundary = (rayCell + vec(0,0) )/ cell_count + crossOffset,其中crossOffset < 0.
crossStep = saturate(crossStep);
vec3 ray = start;
float minZ = ray.z;
float maxZ = ray.z + rayDir.z * maxTraceDistance;
float deltaZ = (maxZ - minZ);
vec3 o = ray;
vec3 d = rayDir * maxTraceDistance;
int startLevel = 2;
int stopLevel = 0;
vec2 startCellCount = vec2(getCellCount(startLevel));
//步进起点所在的单元格。
vec2 rayCell = getCell(ray.xy, startCellCount);
//防止自相交。
ray = intersectCellBoundary(o, d, rayCell, startCellCount, crossStep, crossOffset * 128. * 2. );
int level = startLevel;
int iter = 0;
...
while( level >= stopLevel && ray.z <= maxZ && ++iter < 1000){
//获取纹理分辨率
vec2 cellCount = vec2(getCellCount(level));
//步进起点所在的单元格索引
vec2 oldCellIdx = getCell(ray.xy, cellCount);
//步进起点所在单元格的GbufferDepth
float cell_minZ = getMinimumDepthPlane((oldCellIdx + 0.5) / cellCount, level);
if(cell_minZ == 1.0) return false;//解决SSR测试的问题
//试探步:步进起点的深度小于GbufferDepth,则步进到ray.z >= gbufferDepth的地方,这可能会导致新的tmpRay.xy超过1.0,所以这里只是试探步,实际步进是用intersectCellBoundary这个函数完成。
vec3 tmpRay = (cell_minZ > ray.z) ? intersectDepthPlane(o, d, (cell_minZ - minZ) / deltaZ) : ray;
//此次试探步终点所在单元格的索引
vec2 newCellIdx = getCell(tmpRay.xy, cellCount);
//如果到了第0层级,那么说明马上快要到交点处了,比较深度差值,如果差值大于某个阈值(0.0017),我们还需要在当前层级步进一个单元格。
float thickness = level == 0 ? (ray.z - cell_minZ) : 0.;
//步进起点和终点不在同一个单元格为true。
bool crossed = (thickness > MAX_THICKNESS)|| crossedCellBoundary(oldCellIdx, newCellIdx);
//步进:不在同一个单元格 则寻找最近的一个单元格进行步进,在同一个单元格则步进到试探步的地方。
ray = crossed ? intersectCellBoundary(o, d, oldCellIdx, cellCount, crossStep, crossOffset) : tmpRay;
//不在同一个单元格 则步进距离再次增大,在同一个单元格则距离减小。
level = crossed ? min(MAX_MIPMAP_LEVEL, level + 1): level - 1;
}
...
}tmpRay接收了试探步的位置。下面则是通过crossedCellBoundary(oldCellIdx, newCellIdx)来判断tmpRay是否和起点A在相同单元格。如果不在同一个单元格则crossed为true,我们需要用intersectCellBoundary来使起点A步进到下一个单元格。intersectCellBoundary函数的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23vec3 intersectCellBoundary(
vec3 o,
vec3 d,
vec2 rayCell,
vec2 cell_count,
vec2 crossStep,
vec2 crossOffset
){
//光线所在单元格的下一个单元格
vec2 index = rayCell + crossStep;
//下一个单元格的边界,根据当前level的单元格数量决定
vec2 boundary = index / cell_count;
//边界偏移一点,防止步进时落在边界上。
boundary += crossOffset;
//步进的距离
vec2 delta = boundary - o.xy;
//标准化
delta /= d.xy;
//选择最小被标准化后的步进值,代表朝着 离现在光线所在单元格最近的一个单元格 步进
float t = min(delta.x, delta.y);
//步进后的点
return intersectDepthPlane(o, d, t);
}o为步进起点的位置,d为非单位向量,rayCell为起点A所在的单元格,cell_count为当前Depth
Mipmap层级的分辨率,crossStep为该单元格向下一个单元格步进的向量,crossOffset为微小偏移防止步进后的点落在边界上。下面我还是用图例的形式进一步解释这个函数如何工作的,这里我们忽略z值:

这里o(0,0.125)为光线起点,endPos(1,0.5)为光线终点,c(0.45,0.3)为步进起点,我们要求的点为nextc。光线起点c所在的单元格rayCell(1,1),这里因为d(1,0.375)的两个分量都大于零所以crossStep为(1,1),cell_count则是当前层级的分辨率为(4,4)。
rayCell根据crossStep,移动到下一个单元格,即紫色点所在位置(这里忽略了偏移值)。然后除以cell_count得到它们的相对位置即boundary(0.5,0.5)。
再通过公式(boundary - o.xy) / d.xy来确定归一化的系数t,通过图例和计算我们很容易的观察到,此时x分量的系数t是y分量的0.5倍,即光线d需要走到endPos,nextc的y分量才和boundary的y分量相等,而这并不是我们想要的,所以我们这里选择系数相对较小的来步进,这样通过公式o+t*d就可以准确得到步进到下一个单元格的相对坐标了(这里红色点和蓝色点应该在光线d上面,这里为了取值方便没有画在一起)。
同理当步进起点向反方向步进时,将o和endPos反过来,并且crossStep为(0,0)时也可以得到步进后的点,这里就不再解释了。
还有最后一件事情没做,我们上面讨论的情况只适用于向前追踪,如果向后追踪,即向nearPlane步进,直接用上面的算法会出错。这是因为试探步函数intersectDepthPlane(o, d, (cell_minZ - minZ) / deltaZ),处理不了向后步进的情况,我们看下这个cell_minZ变量,如果是向后步进,这个变量的值只会一直递减,相应的系数t也会一直递减,从而无法完成试探步
步进的工作。但是幸运的是,向后追踪的情况比向前追踪简单,我们只需要用一个方向布尔变量来控制算法流程。
在每次迭代中,我们得到了步进起点所对应的Depth Mipmap场景深度cell_minZ,当场景深度大于步进起点深度时,我们就调用intersectCellBoundary来步进到下一个单元格,而不需要经过试探步来决定。
整个Hi-z算法代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61bool FindIntersection_HiZ(
in SSRay ss_ray,
out vec3 intersection
) {
vec3 start = ss_ray.rayPosInTS;
vec3 rayDir = ss_ray.rayDirInTS;
float maxTraceDistance = ss_ray.maxDistance;
vec2 crossStep = vec2(rayDir.x >= 0.0 ? 1.0 : -1.0, rayDir.y >= 0.0 ? 1.0 : -1.0);
vec2 crossOffset = crossStep / vec2(windowWidth,windowHeight) / 128.;
//假设reflectDir不与屏幕的宽高平行,如果是向前步进一个单元格的距离,boundary = (rayCell + crossStep )/ cell_count + crossOffset,其中crossOffset > 0.
//如果是向后步进一个单元格的距离,boundary = (rayCell + vec(0,0) )/ cell_count + crossOffset,其中crossOffset < 0.
crossStep = saturate(crossStep);
vec3 ray = start;
float minZ = ray.z;
float maxZ = ray.z + rayDir.z * maxTraceDistance;
float deltaZ = (maxZ - minZ);
vec3 o = ray;
vec3 d = rayDir * maxTraceDistance;
int startLevel = 2;
int stopLevel = 0;
vec2 startCellCount = vec2(getCellCount(startLevel));
//步进起点所在的单元格。
vec2 rayCell = getCell(ray.xy, startCellCount);
//防止自相交。
ray = intersectCellBoundary(o, d, rayCell, startCellCount, crossStep, crossOffset * 128. * 2. );
int level = startLevel;
int iter = 0;
bool isBackwardRay = rayDir.z < 0.;
float Dir = isBackwardRay ? -1. : 1.;
while( level >= stopLevel && ray.z * Dir <= maxZ * Dir && ++iter < 1000){
//获取纹理分辨率
vec2 cellCount = vec2(getCellCount(level));
//步进起点所在的单元格索引
vec2 oldCellIdx = getCell(ray.xy, cellCount);
//步进起点所在单元格的GbufferDepth
float cell_minZ = getMinimumDepthPlane((oldCellIdx + 0.5) / cellCount, level);
if(cell_minZ == 1.0) return false;//解决SSR测试的问题
//试探步:步进起点的深度小于GbufferDepth,则步进到ray.z >= gbufferDepth的地方,这可能会导致新的tmpRay.xy超过1.0,所以这里只是试探步,实际步进是用intersectCellBoundary这个函数完成。
vec3 tmpRay = ((cell_minZ > ray.z) && !isBackwardRay) ? intersectDepthPlane(o, d, (cell_minZ - minZ) / deltaZ) : ray;
//此次试探步终点所在单元格的索引
vec2 newCellIdx = getCell(tmpRay.xy, cellCount);
//如果到了第0层级,那么说明马上快要到交点处了,比较深度差值,如果差值大于某个阈值(0.0017),我们还需要在当前层级步进一个单元格。
float thickness = level == 0 ? (ray.z - cell_minZ) : 0.;
//步进起点和终点不在同一个单元格为true。
bool crossed = (isBackwardRay && (cell_minZ > ray.z))||(thickness > MAX_THICKNESS)|| crossedCellBoundary(oldCellIdx, newCellIdx);
//步进:不在同一个单元格 则寻找最近的一个单元格进行步进,在同一个单元格则步进到试探步的地方。
//前向追踪不适合用在后向追踪,如果是backwardRay,没有试探步。cell_minZ > ray.z为true则步进到下一个单元格level + 1,false则保留当前状态level - 1;
ray = crossed ? intersectCellBoundary(o, d, oldCellIdx, cellCount, crossStep, crossOffset) : tmpRay;
//不在同一个单元格 则步进距离再次增大,在同一个单元格则距离减小。
level = crossed ? min(MAX_MIPMAP_LEVEL, level + 1): level - 1;
}
bool intersected = (level < stopLevel);
intersection = intersected ? ray : vec3(0.0);
return intersected;
}thickness是为了让光线穿过物体。不然我们会得到一些错误的结果。
这节的内容将的有点HighLevel,更多细节可以参考Hierarchical-Z
SSR。
如果一切顺利,就会得到下面的效果:

全局光照如何处理在上面World Space Ray Marching SSR已经讲过,这里只需要照着做就行。