Games202 Hw4 IBL and Kulla Conty
最终效果图
每组下面一排球是没用Kulla Conty的对照组,所有球的金属度都为1,粗糙度最小0.05,最大0.95,可以明显看到对照组随着粗糙度增大,会越来越暗,而使用了Kulla Conty的实验组,亮度不会随着粗糙度的增加而衰减,为了使现象更明显这里吧HDR tonemapping功能禁用了!

下面是金材质的Kulla-Conty Approximation效果:

作业总览
- 实现预计算\(E(\mu)\)
- 实现预计算\(E_{avg}\)
- 正确实现PBR材质
- 正确实现Kulla-Conty材质
- 提高1:实现重要性采样的预计算方法
- 提高2:在预计算\(E(\mu)\)时,使用
Split Sum完成预计算工作
个人扩展部分:Image Based Lighting
源码
Webgl代码框架的理解
这部分代码主要解释我们需要的地方,太过于细节的地方本节内容不做解释,只去理解那些能帮助我实现想要效果的代码。
模型加载
1 | |
模型加载主要就看这部分,打了省略的部分不需要去理解。
colorMap获取创建的纹理ID,kD是albedo,只为了观察能量损失和补充直接填1.0就行,CreateConstantTexture用albedo创建一张宽高为1的纹理。
buildKullaContyMaterial是一个异步函数,函数执行完成后就会进入回调部分material.then((data)),data才是函数的返回值。
child.isMesh会判断模型的子节点是否为mesh节点,经过debug发现,该ball模型有4个子节点,也就说会进入回调部分material.then((data))4次。
shader编译
在理解框架shader编译之前需要把材质类型熟悉一下,以PBRMaterial.js为例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Material {
#flatten_uniforms;
#flatten_attribs;
#vsSrc;
#fsSrc;
// Uniforms is a map, attribs is a Array
constructor(uniforms, attribs, vsSrc, fsSrc, frameBuffer) {
this.uniforms = uniforms;
this.attribs = attribs;
this.#vsSrc = vsSrc;
this.#fsSrc = fsSrc;
this.#flatten_uniforms = ['uViewMatrix','uModelMatrix', 'uProjectionMatrix', 'uCameraPos', 'uLightPos'];
for (let k in uniforms) {
this.#flatten_uniforms.push(k);
}
this.#flatten_attribs = attribs;
this.frameBuffer = frameBuffer;
}
setMeshAttribs(extraAttribs) {
for (let i = 0; i < extraAttribs.length; i++) {
this.#flatten_attribs.push(extraAttribs[i]);
}
}
compile(gl) {
return new Shader(gl, this.#vsSrc, this.#fsSrc,
{
uniforms: this.#flatten_uniforms,
attribs: this.#flatten_attribs
});
}
}
class PBRMaterial extends Material {
constructor(albedo, metallic,roughness,irradianceMap,prefilterMap,pbrBrdfLut, vertexShader, fragmentShader) {
super({
'uAlbedoMap': { type: 'texture', value: albedo },
'uMetallic': { type: '1f', value: metallic },
...
// 'uLightPos[4]': { type: '3fv', value: null },
// 'uLightColors[4]': { type: '3fv', value: null },
}, [], vertexShader, fragmentShader);
}
}
async function buildPBRMaterial(albedo, metallic,roughness,irradianceMap,prefilterMap,pbrBrdfLut, vertexPath, fragmentPath) {
let vertexShader = await getShaderString(vertexPath);
let fragmentShader = await getShaderString(fragmentPath);
return new PBRMaterial(albedo, metallic,roughness,irradianceMap,prefilterMap,pbrBrdfLut, vertexShader, fragmentShader);
}Material,子类部分只负责填写对应shader需要uniform的变量,子类用super关键字来对父类进行初始化,随后填写uniform数据全部被保存入父类私有变量#flatten_uniforms中,父类还包含了一些常用uniform变量'uViewMatrix','uModelMatrix'...,这些名字在不同的vertex和fragment中名字都是统一的,可自行修改,数组uniform变量需要自己手动设置,框架没有对这类变量进行解析。
this.#vsSrc和this.#fsSrc保存的shader文件路径,#this.attribs保存的vertexShader的location变量名字,比如:
layout (location = 0) in vec3 aVertexPosition;中的aVertexPosition,所以在vertexShader中不要更改它的名字,名字都是来源于mesh节点,在MeshRender.js文件中会判断mesh节点是否包含该属性名字,有的话就调用该材质的setMeshAttribs函数将名字存入#this.attribs。
在调用compile()函数的时候,shader路径,uniform变量名,attribs变量名字会一同传入new出来的shader对象。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42class Shader {
constructor(gl, vsSrc, fsSrc, shaderLocations) {
this.gl = gl;
const vs = this.compileShader(vsSrc, gl.VERTEX_SHADER);
const fs = this.compileShader(fsSrc, gl.FRAGMENT_SHADER);
this.program = this.addShaderLocations({
glShaderProgram: this.linkShader(vs, fs),
}, shaderLocations);
}
compileShader(shaderSource, shaderType) {
const gl = this.gl;
var shader = gl.createShader(shaderType);
...
return shader;
};
linkShader(vs, fs) {
const gl = this.gl;
var prog = gl.createProgram();
...
return prog;
};
addShaderLocations(result, shaderLocations) {
const gl = this.gl;
result.uniforms = {};
result.attribs = {};
if (shaderLocations && shaderLocations.uniforms && shaderLocations.uniforms.length) {
for (let i = 0; i < shaderLocations.uniforms.length; ++i) {
result.uniforms = Object.assign(result.uniforms, {
[shaderLocations.uniforms[i]]: gl.getUniformLocation(result.glShaderProgram, shaderLocations.uniforms[i]),
});
}
}
if (shaderLocations && shaderLocations.attribs && shaderLocations.attribs.length) {
for (let i = 0; i < shaderLocations.attribs.length; ++i) {
result.attribs = Object.assign(result.attribs, {
[shaderLocations.attribs[i]]: gl.getAttribLocation(result.glShaderProgram, shaderLocations.attribs[i]),
});
}
}
return result;
}
}gl.createProgram()这个函数返回shader的ID,该ID存储在addShaderLocations()这个函数中result对象里面,{ glShaderProgram: this.linkShader(vs, fs) }这里是对result对象的初始化,后面又加了两个成员变量result.uniforms和result.attribs。
重点是这个函数addShaderLocations(),result.uniforms和result.attribs存储的是一系列键值对,key是之前传入的uniform变量名,value是location后得到ID,result.attribs同理。
所以在MeshRender对象中,进行gl.useProgram(),gl.uniform(),gl.enableVertexAttribArray()操作时,只需要所以用变量名来索引shader.program的shaderID,uniformID,attribsID以及即可,该program就对应上面说的result的内容。
知道这些以后我们就可以自行对shader进行uniform,和useProgram操作,对于需要手动设置uniform变量如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18for (let l = 0; l < this.lights.length; l++) {
...
// Camera pass
for (let i = 0; i < this.meshes.length; i++) {
if(this.meshes[i].materialName == "KullaContyMaterial" || this.meshes[i].materialName == "PBRMaterial"){
let ID = this.meshes[i].shader.program.glShaderProgram;
this.gl.useProgram(ID);
gl.uniform3fv(gl.getUniformLocation(
ID, "uLightPos" + "[" + l + "]"),
this.lights[l].entity.lightPos);
gl.uniform3fv(gl.getUniformLocation(
ID, "uLightColors" + "[" + l + "]"),
this.lights[l].entity.lightRadiance);
}
this.meshes[i].draw(this.camera);
}
}
IBL
IBL的实现流程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37//ibl
let envCubemap,irradianceMap,prefilterMap;
let pbrBrdfLutObj;
let hdrObj = new Texture(gl);
//加载HDR文件
async function loadTexture() {
return new Promise((resolve) => {
new THREE.RGBELoader().load("assets/winter_sky_1k.hdr", function(texture) {
console.log("HDR Loaded");
resolve(texture);
});
});
}
async function integral() {
let hdrData = await loadTexture();
let data = hdrData.image.data;
let width = hdrData.image.width;
let height = hdrData.image.height;
gl.bindTexture(gl.TEXTURE_2D, hdrObj.texture);
gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, width, height, 0, gl.RGBA, gl.UNSIGNED_BYTE,new Uint8Array(data));
////debug texture
// gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, 1, 1, 0, gl.RGBA, gl.UNSIGNED_BYTE,
// new Uint8Array([0, 0, 255, 255]));
gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_WRAP_S, gl.CLAMP_TO_EDGE);
gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_WRAP_T, gl.CLAMP_TO_EDGE);
gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);
gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER, gl.LINEAR);
gl.bindTexture(gl.TEXTURE_2D, null);
getErrorMessage(gl,"engine.js");
let ibl = new IBL(gl,hdrObj.texture);
await ibl.init();
envCubemap = ibl.caculateEnvCubemap();
irradianceMap = ibl.caculateIrradianceMap();
prefilterMap = ibl.caculatePrefilterMap();
pbrBrdfLutObj = ibl.caculateLut();
}
await integral();HDR文件,将HDR的内容载入一张2D纹理中(hdrObj),然后根据纹理生成environmentCubemap(envCubemap),然后根据Cubemap预计算漫反射项(irradianceMap)的光照部分,镜面反射项的光照部分(prefilterMap)以及对BRDF本身的预计算(pbrBrdfLutObj),然后在shader中直接查表完成环境光Cook-Torrance反射模型的积分。
注意gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, width, height, 0, gl.RGBA, gl.UNSIGNED_BYTE,new Uint8Array(data));这个函数读取数据的类型不能像Opengl那样填gl.FLOAT,不然会报错,可以用这个函数来检测getErrorMessage()。如果非得使用gl.Float可以像作业三那样添加gl.getExtension('EXT_color_buffer_float')扩展。
从等距柱状投影到立方体贴图
HDR文件载入2D纹理后就是等距柱状投影图(Equirectangular Map),我们要做的就是将这张2D纹理转换成Cubemap。
这里用UV
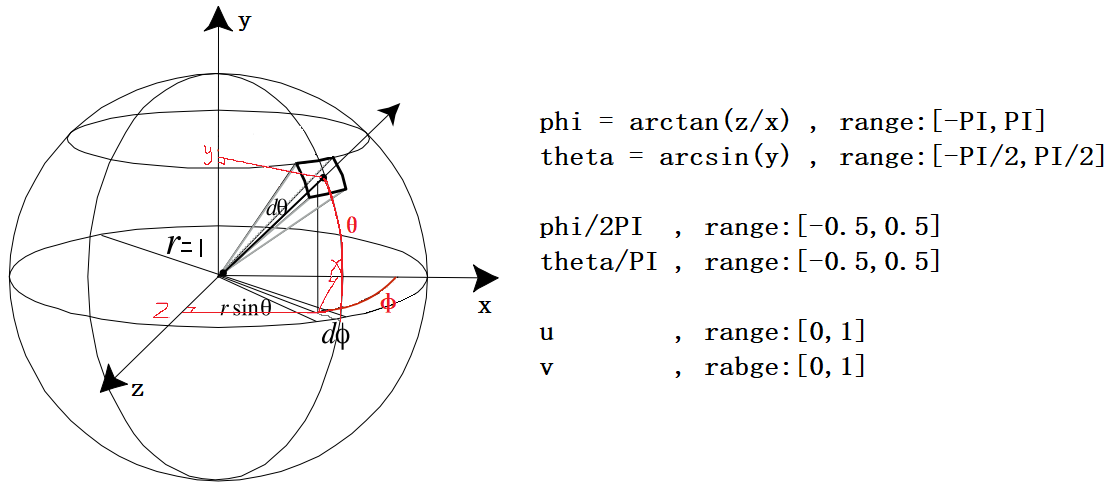
mapping中的技术,从球面上找到UV坐标。从笛卡尔坐标系转球坐标系然后映射到[0,1]区间去采样等距柱状图,在右手坐标系进行,phi逆时针旋转。公式如下:
\[
\begin{align}
u=0.5+\frac{\arctan(p_{z},p_{x})}{2\pi} \\
v=0.5+\frac{\arcsin(p_{y})}{\pi} \tag{1}
\end{align}
\] 解释如下:
 代码如下:
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23const vec2 invAtan = vec2(0.1591, 0.3183);
// hdr文件存储每个浮点值的方式
// 每个通道存储 8 位,再以 alpha 通道存放指数
// 因此利用这种方式解码
vec3 hdrDecode(vec4 encoded){
float exponent = encoded.a * 256.0 - 128.0;
vec3 mantissa = encoded.rgb;
return exp2(exponent) * mantissa;
}
vec2 SampleSphericalMap(vec3 v)
{
vec2 uv = vec2(atan(v.z, v.x), asin(v.y));
uv *= invAtan;
uv += 0.5;
return uv;
}
void main()
{
vec2 uv = SampleSphericalMap(normalize(WorldPos));
vec4 enCodeColor = texture(uEquirectangularMap,uv).rgba;
vec3 deCodeColor = hdrDecode(enCodeColor);
fragColor = vec4(vec3(deCodeColor), 1.0);
}
环境光Cook-Torrance反射方程的预计算
快速浏览一下反射方程:
\[
L_{o}(p,w_{o})=\int_{\Omega}^{}(kd\frac{c}{\pi}+ks\frac{DFG}{4(w_{o}\cdot
n)(w_{i}\cdot n)})L_{i}(p,w_{i})n\cdot w_{i}dw_{i} \tag{2}
\] 该公式的解释可以参考Opengl
Pbr。值得一提的是公式中ks和Fresnel项指代的同一件事情,所以ks可以省略,其中o代表出射方向也就是我们看到的方向,i是入射方向即光照方向。
漫反射光照的预计算
仔细观察会发现BRDF的漫反射kd和镜面ks项是相互独立的,我们可以将积分分成两部分:
\[
L_{o}(p,w_{o})=\int_{\Omega}(kd\frac{c}{\pi})L_{i}(p,w_{i})n\cdot
w_{i}dw_{i}+\int_{\Omega}(\frac{DFG}{4(w_{o}\cdot n)(w_{i}\cdot
n)})L_{i}(p,w_{i})n\cdot w_{i}dw_{i} \tag{3}
\]
前这部分才是本节的重点,让我们在化简一下(颜色c,漫反射率kd,和π在整个积分是常数):
\[
L_{o}(p,w_{o})=(kd\frac{c}{\pi})\int_{\Omega}L_{i}(p,w_{i})n\cdot
w_{i}dw_{i} \tag{4}
\]
经过简化有可以发现,积分目前只跟wi有关(假设物体上的点p位于立方体中间,N为p与立方体上某点的连线),由于是漫反射在半球上的积分,其入射方向是均匀的来自半球的四面八方。
积分参考Opengl的方法:对于立方体贴图的每个纹素,在纹素所代表的方向的半球Ω内生成固定数量的采样向量,并对采样结果取平均值。数量固定的采样向量将均匀地分布在半球内部。注意,积分是连续函数,在采样向量数量固定的情况下离散地采样只是一种近似计算方法,我们采样的向量越多,就越接近正确的结果。
纹素所代表的方向的半球Ω内生成固定数量的采样向量,图解如下:
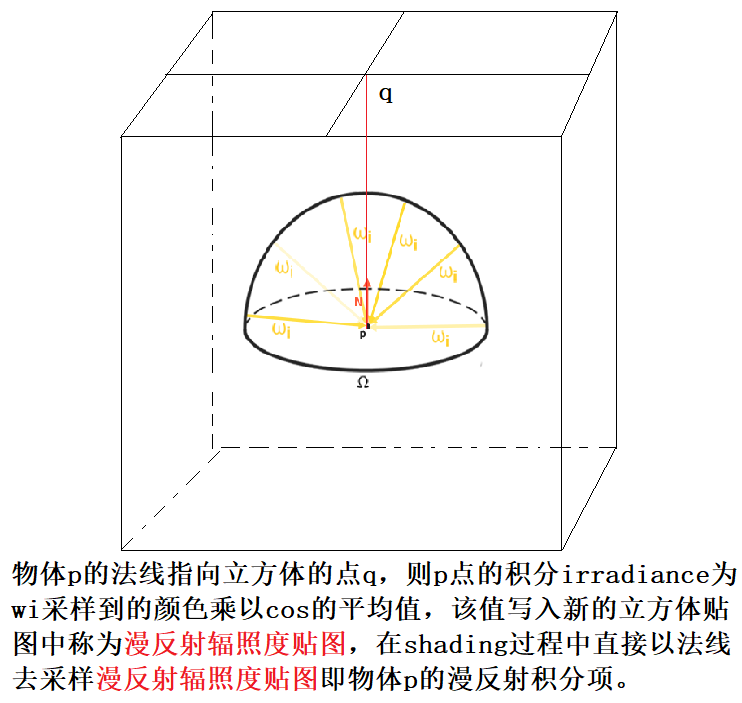
反射方程的积分∫是围绕立体角dw旋转,而这个立体角相当难以处理。为了避免对难处理的立体角求积分,我们使用球坐标θ和ϕ来代替立体角。公式如下:
\[
\begin{align}
L_{o}(p,\phi_{o},\theta_{o})=kd\frac{c}{\pi}\int_{\phi=0}^{2\pi}\int_{\theta=0}^{\frac{1}{2}\pi}L_{i}(p,\phi_{i},\theta_{i})\cos(\theta_{i})\sin(\theta_{i})d\theta
d\phi\\
=kd\frac{c}{\pi}\frac{2\pi}{n1}\frac{\pi}{2\cdot
n2}\sum_{m=0}^{n1}\sum_{n=0}^{n2}L_{i}(p,\phi_{m},\theta_{n})\cos(\theta_{n})\sin(\theta_{n})\\
=kd\frac{c\pi}{n1\cdot
n2}\sum_{m=0}^{n1}\sum_{n=0}^{n2}L_{i}(p,\phi_{m},\theta_{n})\cos(\theta_{n})\sin(\theta_{n})
\tag{5}
\end{align}
\]
该结果由蒙特卡洛积分所得,φ的概率密度为1/2PI,θ的概率密度为2/PI,其中添加的sin(θ)是为了权衡较高半球区域的较小采样区域的贡献度如图:
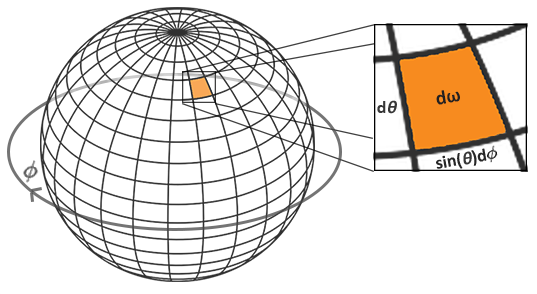
给定每个片段的积分球坐标,对半球进行离散采样,过程代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26const float PI = 3.14159265359;
void main()
{
vec3 N = normalize(WorldPos);
vec3 irradiance = vec3(0.0);
// tangent space calculation from origin point
vec3 up = vec3(0.0, 1.0, 0.0);
vec3 right = normalize(cross(up, N));
up = normalize(cross(N, right));
float sampleDelta = 0.025;
float nrSamples = 0.0f;
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{
for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
{
// spherical to cartesian (in tangent space)
vec3 tangentSample = vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
// tangent space to world
vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N;
irradiance += texture(uEnvironmentMap, sampleVec).rgb * cos(theta) * sin(theta);
nrSamples++;
}
}
irradiance = PI * irradiance * (1.0 / float(nrSamples));
FragColor = vec4(irradiance, 1.0);
}TBN矩阵将该向量转至世界空间。最后得到漫反射辐照度贴图如下:

糊的很,根本没有细节可言。
SplitSum和GGX重要性采样
为了理解,我们回顾一下反射方程,但这次只关注镜面反射部分(在上一节中已经剥离了漫反射部分):
\[
L_{o}(p,w_{o})=\int_{\Omega}(\frac{DFG}{4(w_{o}\cdot n)(w_{i}\cdot
n)})L_{i}(p,w_{i})n\cdot w_{i}dw_{i} \tag{6}
\]
对这部分积分进行预计算有个棘手的地方,它不仅依赖wi还依赖wo,我们不可能吧wi和wo的每种组合都进行预计算(wi(θ,φ),wo(θ,φ),F0,roughness,一共六个维度也无法预计算),所以Epic Games提出了一个新的解决方法split
sum:
\[
\begin{align}
\int_{\Omega}(\frac{DFG}{4(w_{o}\cdot n)(w_{i}\cdot
n)})L_{i}(p,w_{i})n\cdot w_{i}dw_{i}\\
\approx\frac{1}{N}\sum_{k=1}^{N}\frac{L_{i}(p,w_{ik})f_{r}(p,w_{ik},w_{ok})\cos(\theta_{ik})}{p(w_{ik},w_{ok})}\\
\approx(\frac{1}{N}\sum_{k=1}^{N}L_{i}(p,w_{ik}))(\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{ik},w_{ok})\cos(\theta_{ik})}{p(w_{ik},w_{ok})})
\tag{7}
\end{align}
\]
该式子左边是一个求和,右边是蒙特卡洛积分,左右分别为两维度,可以直接查表。左边wi是两维度好理解,右边两维度我在后面章节解释。我们分别对这两部分进行预计算就可以解决上面棘手的部分。
但是它们都是建立在GGX重要性采样的基础上,先介绍一下重要性采样:
我们使用球面坐标生成均匀分布在半球Ω上的采样向量,以对环境贴图进行卷积。虽然这个方法非常适用于辐照度,但对于镜面反射效果较差。镜面反射依赖于表面的粗糙度,反射光线可能比较松散,也可能比较紧密,但是一定会围绕着反射向量r,除非表面极度粗糙:

所有可能出射的反射光构成的形状称为镜面波瓣。随着粗糙度的增加,镜面波瓣的大小增加;随着入射光方向不同,形状会发生变化。因此,镜面波瓣的形状高度依赖于材质。
在微表面模型里给定入射光方向,则镜面波瓣指向微平面的半向量的反射方向。考虑到大多数光线最终会反射到一个基于半向量的镜面波瓣内,采样时以类似的方式选取采样向量是有意义的,因为大部分其余的向量都被浪费掉了。根据表面粗糙度生成法线N,然后以镜面反射的形式计算出采样方向的过程称为重要性采样。
要理解重要性采样需要先理解逆变换采样,逆变换采样是用range为[0,1]之间的均匀随机数来生成服从pdf的样本,其过程如下:
1.从均匀分布U[0,1]中产生一个随机数ui
2.计算\(x_{i}=F_{X}^{-1}(u_{i})\)作为采样结果
其中\(F_{X}(x)\)为CDF(累积分布函数)所有的CDF中,在x趋近最小值时,CDF趋近于0,当x趋近最大值时,CDF趋近与1。
\(f_{X}(x)\)为随机变量X的pdf(概率密度函数)。这是它们的关系\(F_{X}(x)=\int_{-\infty}^{x}f_{X}(u)du\)
\(F_{X}^{-1}(x)\)为cdf的反函数,只有单调非减的函数才有反函数。
GGX重要性采样用的概率密度函数为D(h)dot(n,h),其在球坐标系下的概率密度函数为:
\[
p_{h}(\theta,\phi)=\frac{\alpha^{2}\cos(\theta)\sin(\theta)}{\pi((\alpha^{2}-1)\cos^{2}(\theta)+1)^{2}}
\tag{8}
\] 分别求θ和φ的边缘概率密度函数(pdf): \[
\begin{align}
p_{h}(\theta)=\int_{0}^{2\pi}p_{h}(\theta,\phi)d\phi=\frac{2\alpha^{2}\cos(\theta)\sin(\theta)}{((\alpha^{2}-1)\cos^{2}(\theta)+1)^{2}}
\tag{9}
\end{align}
\] \[
\begin{align}
p_{h}(\phi)=\int_{0}^{\frac{\pi}{2}}\frac{\alpha^{2}\cos(\theta)\sin(\theta)}{\pi((\alpha^2-1)\cos^{2}(\theta)+1)^{2}}d\theta\\
=-\frac{\alpha^{2}}{2\pi}\int_{0}^{\frac{\pi}{2}}\frac{-2\cos(\theta)\sin(\theta)}{((\alpha^2-1)\cos^{2}(\theta)+1)^{2}}d\theta\\
=\frac{\alpha^{2}}{2\pi}\int_{\frac{\pi}{2}}^{0}\frac{1}{((\alpha^2-1)\cos^{2}(\theta)+1)^{2}}d(\cos^{2}\theta)\\
=\frac{\alpha^{2}}{2\pi}\int_{0}^{1}\frac{1}{((\alpha^{2}-1)t+1)^{2}}dt\\
\end{align}
\] 令x=(α^2-1)t+1 \[
\begin{align}
=\frac{\alpha^{2}}{2\pi(\alpha^2-1)}\int_{1}^{\alpha^2}\frac{1}{x^{2}}dx
\\
=\frac{\alpha^{2}}{2\pi(1-\alpha^2)}\frac{1}{x}\vert_{1}^{\alpha^2} \\
=\frac{1}{2\pi} \tag{10}
\end{align}
\] 再分别求θ和φ的累计分布函数(cdf):
\[
P_{h}(\phi)=\int_{0}^{\phi}\frac{1}{2\pi}dt=\frac{\phi}{2\pi} \tag{11}
\] \[
\begin{align}
P_{h}(\theta)=\int_{0}^{\theta}\frac{2\alpha^{2}\cos(t)\sin(t)}{((\alpha^{2}-1)\cos^{2}(t)+1)^{2}}dt
\\
=\alpha^{2}\int_{\theta}^{0}\frac{1}{((\alpha^2-1)\cos^{2}(t)+1)^{2}}d(\cos^{2}(t))
\\
=\frac{\alpha^2}{\alpha^2-1}\int_{\alpha^2}^{(\alpha^2-1)\cos^{2}(\theta)+1}-\frac{1}{x^{2}}dx
\\
=\frac{\alpha^2}{\alpha^2-1}\frac{1}{x}\vert_{\alpha^{2}}^{(\alpha^2-1)\cos^{2}(\theta)+1}
\\
=\frac{\alpha^{2}}{\alpha^{2}-1}\cdot
(\frac{1}{(\alpha^2-1)\cos^{2}(\theta)+1}-\frac{1}{\alpha^{2}}) \tag{12}
\end{align}
\]
反函数就是函数值域Y和定义域X的映射关系翻转一下。
均匀的从U[0,1]中取出两个随机数\(X_{1}\)和\(X_{2}\),则我们要的采样θ和φ为:
\[
\phi=2\pi X_{1} \tag{13}
\] \[
\theta=\arccos\sqrt{\frac{1-X_{2}}{X_{2}(\alpha^{2}-1)+1}} \tag{14}
\] 对应代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
float a = roughness*roughness;
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
// from spherical coordinates to cartesian coordinates - halfway vector
vec3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// from tangent-space H vector to world-space sample vector
vec3 up = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangent = normalize(cross(up, N));
vec3 bitangent = cross(N, tangent);
vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
镜面反射光照的预计算
上节内容提到用Split Sum来分割镜面反射的光照和BRDF部分以避免去求wi和wo所有组合下的积分。本节重要点放在镜面反射光照的预计算,我们再看下这部分的公式:
\[
\frac{1}{N}\sum_{k=1}^{N}L_{i}(p,w_{ik}) \tag{15}
\]
这里可以看做是一次求和取平均。还有一个问题就是,这里的wi不仅需要GGX重要性采样得到的符合D(h)dot(n,h)概率密度函数的微表面法线方向,还需要视角方向V,但是我们并不能提前知道V是什么方向,这里Epic Games再一次假设,即v=r=n。这种各向同性假设是第二个近似来源,不幸的是,这意味在掠入射角时不会得到长反射效果:

与分裂和近似相比,这实际上是我们IBL解的较大误差源。代码中通过cosθlk加权可以获得更好的结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36void main()
{
vec3 N = normalize(WorldPos);
// make the simplifying assumption that V equals R equals the normal
vec3 R = N;
vec3 V = R;
const uint SAMPLE_COUNT = 1024u;
vec3 prefilteredColor = vec3(0.0);
float totalWeight = 0.0;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
// generates a sample vector that's biased towards the preferred alignment direction (importance sampling).
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, uRoughness);
vec3 L = normalize(2.0 * dot(V, H) * H - V);
//COS weight can increase image quality
float NdotL = max(dot(N, L), 0.0);
if(NdotL > 0.0)
{
// sample from the environment's mip level based on roughness/pdf
float D = DistributionGGX(N, H, uRoughness);
float NdotH = max(dot(N, H), 0.0);
float HdotV = max(dot(H, V), 0.0);
float pdf = D * NdotH / (4.0 * HdotV) + 0.0001;
float resolution = 512.0; // resolution of source cubemap (per face)
float saTexel = 4.0 * PI / (6.0 * resolution * resolution);
float saSample = 1.0 / (float(SAMPLE_COUNT) * pdf + 0.0001);
//sample solid angle ratio to pixel solid angle
float mipLevel = uRoughness == 0.0 ? 0.0 : 0.5 * log2(saSample / saTexel);
prefilteredColor += textureLod(uEnvironmentMap, L, mipLevel).rgb * NdotL;
totalWeight += NdotL;
}
}
prefilteredColor = prefilteredColor / totalWeight;
FragColor = vec4(prefilteredColor, 1.0);
}pdf推导过程如下,图片来源于2007年论文:
\[
p_{o}(\theta,\phi)=p_{h}(\theta,\phi)\cdot\lVert\frac{\partial
w_{h}}{\partial w_{o}}\rVert \tag{16}
\] 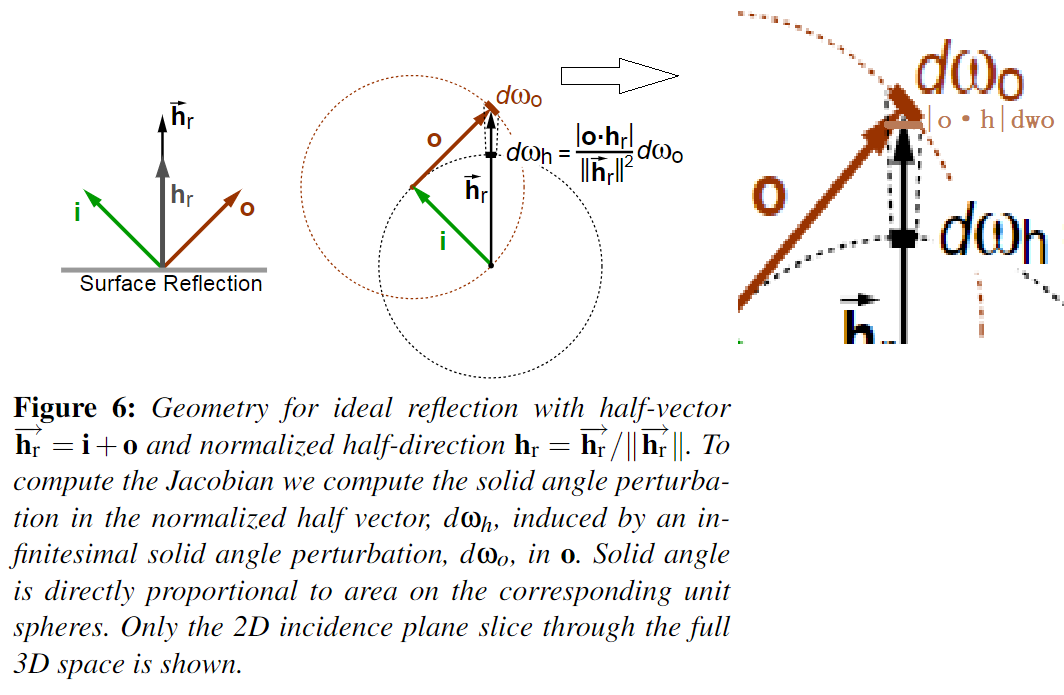
\[
\begin{align}
\lVert\frac{\partial w_{h}}{\partial w_{o}}\rVert=\frac{\vert o\cdot
h\vert}{\lVert\vec{h}\rVert^{2}} \\
=\frac{\vert o\cdot h\vert}{\lVert 2(o\cdot h)h\rVert^{2}}
=\frac{\vert o\cdot h\vert}{4(o\cdot h)^{2}\lVert
h\rVert^{2}}=\frac{1}{4\vert o\cdot h\vert} \tag{17}
\end{align}
\]
其中i,o和没箭头的h,都是归一化后的向量。这只是反射模型的pdf,以同样的计算方法论文作者还给出了折射的pdf,感兴趣可以去看下。需要注意的是这里推导涉及的i,o和代码中的v,L没关系,只是单纯用来推导的,一般来说我们视i为光照方向,o为视角方向。
代码中采样是对uEnvironmentMap的mipmap来采样,而不是直接去获取清晰度最高的uEnvironmentMap,这样做的原因是pdf越低,样本所对应的环境贴图中要平均的纹理像素数就越多,使用的mipmap层级应该越大,mimap第0层级被平均的纹理像素就越多,这可以做到少采样数量达到多采样数量的效果,并减少伪影。我们用与样本相关的实体角来定义这种关系,计算方法是pdf与样本总数N之间乘积的倒数:
\[
\Omega_{s}=\frac{1}{N\cdot p_{L}(\theta,\phi)} \tag{18}
\]
该式子表示采样方向所对应的环境贴图中像素数的多少(采样立体角的大小)。我们还需要知道立方体贴图中一个像素对应的立体角是多大,我们这里是求单位球表面积比上立方体分辨率:
\[
\Omega_{p}=\frac{d(u)}{w\cdot h} \tag{19}
\]
原文这个d(u)是计算从半球的单位面积到纹理上的单位面积的变化速率(换句话说,计算映射的畸变率),原文d(u)是应用在另一种采样方式,不是在立方体贴图上面进行的采样,和我们这里不一样,我们这里直接算立方体贴图上一个像素对应的立体角大小就行。那d(u)直接就是单位球的表面积4π。
最后用下面这个公式计算mipmap层数:
\[
level=max[\frac{1}{2}\log_{2}\frac{\Omega_{s}}{\Omega_{p}},0] \tag{20}
\]
最后计算完的prefilteredColor根据粗糙度[0,1],分别存入prefilterMap的5层mipmap中,在最后shading过程中,根据粗糙度来获取prefilteredColor层数。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24gl.bindFramebuffer(gl.FRAMEBUFFER, captureFBO);
const maxMipLevels = 5;
for (let mip = 0; mip < maxMipLevels; ++mip)
{
// reisze framebuffer according to mip-level size.
let mipWidth = 128 * Math.pow(0.5, mip);
let mipHeight = 128 * Math.pow(0.5, mip);
gl.bindRenderbuffer(gl.RENDERBUFFER, captureRBO);
gl.renderbufferStorage(gl.RENDERBUFFER, gl.DEPTH_COMPONENT24, mipWidth, mipHeight);
gl.viewport(0, 0, mipWidth, mipHeight);
let roughness = mip / (maxMipLevels - 1);
gl.uniform1f(this.prefilterShader.program.uniforms["uRoughness"],roughness);
for (let i = 0; i < 6; ++i)
{
gl.uniformMatrix4fv(
this.prefilterShader.program.uniforms["uViewMatrix"],
false,
this.captureViews[i]);
gl.framebufferTexture2D(gl.FRAMEBUFFER, gl.COLOR_ATTACHMENT0, gl.TEXTURE_CUBE_MAP_POSITIVE_X + i, this.prefilterMap, mip);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
this.renderCube();
}
}
gl.bindFramebuffer(gl.FRAMEBUFFER, null);

预计算BRDF
有了上面的基础,这部分内容就比较简单了,快速看一遍公式:
\[
\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{ik},w_{ok})\cos(\theta_{ik})}{p(w_{ik},w_{ok})}
\tag{21}
\]
上文说到镜面反射方程有六个维度wi(θ,φ),wo(θ,φ),F0,roughness,由于光照部分我们已经处理过了,而此时BRDF的wi和wo都是和n绑定在一起的,那这里BRDF就只剩下4个维度wi·n,wo·n,F0,roughness,由于重要性采样可以由wo生成服从D(h)dot(n,h)概率密度函数的wi,则维度可以再降到3个wo·n,F0,roughness,再将Fresnel项拆分成两部分,F0也可以移出积分范围,维度再降到2个wo·n,roughness,这样就可以愉快的打表了😆!下面是拆分过程,我这里把k角标去掉了方便观看:
\[
\begin{align}
\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})\cos(\theta_{i})}{p(w_{i},w_{o})}
\\
=\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})F(w_{o},h)\cos(\theta_{i})}{F(w_{o},h)p(w_{i},w_{o})}
\\
=\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}(F0+(1-F0)(1-w_{o}\cdot
h)^{5})\cos(\theta_{i})
\end{align}
\] 这里用α代替(1-wo·h)^5:
\[
\begin{align}
=\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}(F0+(1-F0)\alpha)\cos(\theta_{i})
\\
=\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}(F0*(1-\alpha)+\alpha)\cos(\theta_{i})
\\
=\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}F0*(1-\alpha)\cos(\theta_{i})+\frac{1}{N}\sum_{k=1}^{N}\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}\alpha\cos(\theta_{i})
\tag{22}
\end{align}
\] 可以看到这两部分都包含一个共同项:
\[
\frac{f_{r}(p,w_{i},w_{o})}{F(w_{o},h)p(w_{i},w_{o})}\cos(\theta_{i})
\]
我们将其化简一下,其中pdf=D * NdotH / (4.0 * VdotH):
\[
\begin{align}
=\frac{DG\cos(\theta_{i})}{4\cos(\theta_{o})\cos(\theta_{i})}\frac{4(o\cdot
h)}{D(n\cdot h)} \\
=\frac{G(o\cdot h)}{(o\cdot n)(n\cdot h)} \tag{23}
\end{align}
\] 带入(22)式中得:
\[
F0*\frac{1}{N}\sum_{k=1}^{N}\frac{G(o\cdot h)}{(o\cdot n)(n\cdot
h)}(1-(1-(w_{o}\cdot h)^{5}))+\frac{1}{N}\sum_{k=1}^{N}\frac{G(o\cdot
h)}{(o\cdot n)(n\cdot h)}(1-(w_{o}\cdot h)^{5}) \tag{24}
\] 代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34vec2 IntegrateBRDF(float NdotV, float roughness)
{
vec3 V;
V.x = sqrt(1.0 - NdotV*NdotV);
V.y = 0.0;
V.z = NdotV;
float A = 0.0;
float B = 0.0;
vec3 N = vec3(0.0, 0.0, 1.0);
const uint SAMPLE_COUNT = 1024u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
// generates a sample vector that's biased towards the
// preferred alignment direction (importance sampling).
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
vec3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(L.z, 0.0);
float NdotH = max(H.z, 0.0);
float VdotH = max(dot(V, H), 0.0);
if(NdotL > 0.0)
{
float G = GeometrySmith(N, V, L, roughness);
float G_Vis = (G * VdotH) / (NdotH * NdotV);
float Fc = pow(1.0 - VdotH, 5.0);
//pdf = D * NdotH / (4.0 * HdotV);
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
A /= float(SAMPLE_COUNT);
B /= float(SAMPLE_COUNT);
return vec2(A, B);
}
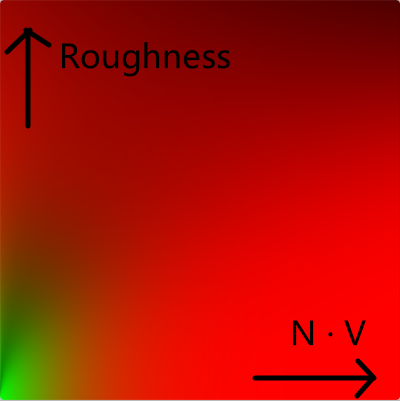
代码中debug出的样子如下:

完成IBL反射
对上面完成的三部分预计算纹理进行查表,即环境光Cook-Torrance反射方程的积分值。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20vec3 fresnelSchlickRoughness(vec3 F0, vec3 V, vec3 N,float roughness){
return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - max(dot(N,V),0.0), 5.0);
}
...
//以环境光作为IBL
vec3 F = fresnelSchlickRoughness(F0,V,N,uRoughness);
vec3 kD = (vec3(1.0) - F) * (1.0 - uMetallic);
//漫反射光照项
vec3 irradiance = texture(uIrradianceMap,N).rgb;
vec3 diffuse = irradiance * albedo;
//以确保不会对一个没有数据的mip级别采样
const float MAX_REFLECTION_LOD = 4.0;
//镜面反射光照项
vec3 prefilteredColor = textureLod(uPrefilterMap,R,uRoughness * MAX_REFLECTION_LOD).rgb;
//BRDF项
vec2 brdf = texture(uPbrBrdfLUT,vec2(max(dot(N,V),0.0),uRoughness)).rg;
//split sum
vec3 specular = prefilteredColor * (F0 * brdf.r + brdf.g);
//环境光Cook-Torrance反射方程的积分值
vec3 ambient = (kD * diffuse + specular) * uAo;fresnelSchlickRoughness函数,是由于环境光来自在半球内所有围绕着法线N的方向,没有单一的半向量去决定菲涅尔因子。为了仍然能模拟菲涅尔,这里采用了法线和视线的夹角。之前的算法采用了受表面粗糙度影响的微平面半向量,作为菲涅尔方程的输入。这里我们加入粗糙度来权衡这一损失。
然后将ambient加到正常的PBR模型上就大功告成了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36vec3 albedo = pow(texture(uAlbedoMap, vTexCoords).rgb,vec3(2.2));
vec3 N = normalize(vNormal);
vec3 V = normalize(uCameraPos - vWorldPos);
vec3 R = reflect(-V, N);
vec3 F0 = vec3(0.04);
F0 = mix(F0, albedo, uMetallic);
vec3 Lo = vec3(0.0);
for (uint i = 0u;i < 4u;++i){
vec3 L = normalize(uLightPos[i] - vWorldPos);
vec3 H = normalize(V + L);
// float distance = length(uLightPos[i] - vWorldPos);
// float attenuation = 1.0 / (distance * distance);
vec3 radiance = uLightColors[i] * 1.0;
//Cook-Torrance BRDF
float NDF = DistributionGGX(N, H, uRoughness);
float G = GeometrySmith(N, V, L, uRoughness);
vec3 F = fresnelSchlick(F0, V, H);
float NdotL = max(dot(N,L),0.0);
float NdotV = max(dot(N,V),0.0);
vec3 numerator = NDF * G * F;
float denominator = max((4.0 * NdotL * NdotV), 0.0000001);
vec3 specular = numerator / denominator;
//Reference opengl pbr
vec3 diffuse = (vec3(1.0)-F) * (1.0 - uMetallic) * albedo / PI;
// Lo += ( diffuse + specular) * radiance * NdotL;
Lo += (specular) * radiance * NdotL;
}
...
vec3 color = ambient + Lo;
// HDR tonemapping
color = color / (color + vec3(1.0));
// gamma correct
color = pow(color, vec3(1.0/2.2));
FragColor = vec4(color, 1.0);kulla Conty方法这里吧diffuse项去掉。
一切顺利的话,会得到下面的效果:

Kulla Conty Approximation
预计算E(μ)和E_avg
在引入Kulla Conty方法之前,我们看下Cook-Torrance反射方程的G项:
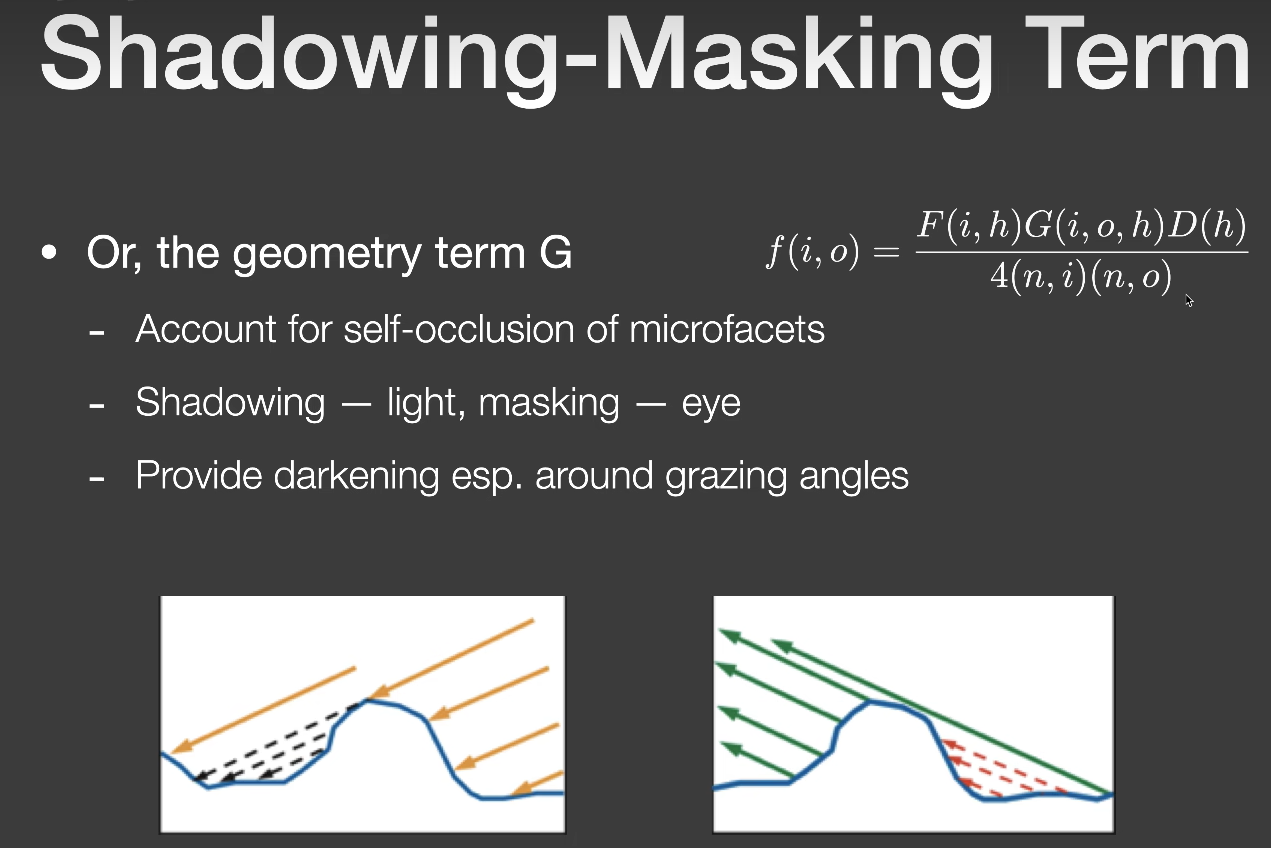
G项考虑了微表面模型的自遮挡现象,在垂直角度看微表面时,几乎没有自遮挡现象,而在掠射角方向看向微表面时,自遮挡现象就会很严重,这是符合物理现象的。但是G项只考虑了光线在微表面上一次反射后的结果,这就导致必定会有一部分参与后续弹射的光线未被考虑进去,当粗糙度越高,沟壑越大后续弹射的光线占比越大能量损失就越多。而kulla conty方法就是为了弥补这部分损失的能量。
考虑Kulla Conty方法时,首先我们需要知道有多少能量丢失了,如果只考虑一次反射,那丢失的能量就是1 - 一次反射。而微表面反射模型本来也就是只考虑了一次的反射,我们假设所有入射方向Li的radiance都为1,则一次反射后我们能看到的能量为:
\[
E(p,w_o)=\int_{\Omega+}\frac{DG}{4(w_o\cdot n)(w_i\cdot n)}n\cdot
w_idw_i \tag{25}
\]
由于这里考虑的全反射,F自然就1,然后我们设μi=cos(wi):
\[
E(\mu_o)=\int_{0}^{2\pi}\int_{0}^{1}f(\mu_o,\mu_i,\phi)\mu_id\mu_id\phi
\tag{26}
\]
这里θ由π/2到0。闫老师课上讲的是用sinθ去替换,但是后面计算sinθ说不通,而不论sinθ替换还是conθ,其推导出的公式都是一样,不同的是sinθ,θ由0到π/2。
得到了E(μo)后,那我们就可以设计另一个BRDF使得其积分的结果为1-E(μo),然后将结果加到原有的BRDF上面,这样就不会有能量损失了。
这个新设计的BRDF就是:
\[
f_{ms}(\mu_o,\mu_i)=\frac{(1-E(\mu_o))(1-E(\mu_i))}{\pi(1-E_{avg})}
\tag{27}
\]
其中E_avg是函数E(μ)在区间[0,1]的平均值:
\[
\begin{align}
E_{avg}=\frac{\int_{0}^{1}E(\mu)\mu d\mu}{\int_{0}^{1}\mu d\mu} \\
=2\int_{0}^{1}E(\mu)\mu d\mu \tag{28}
\end{align}
\] 其正确性参考课堂上给的过程: 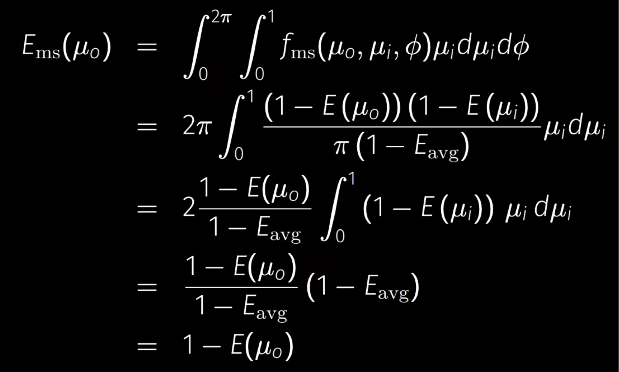
该新设计的BRDF中有两个积分值,我们同样采用打表的形式,把积分值存到一张纹理中。E(μ)的积分值我们同样使用重要性采样来保证结果的正确性,其代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28Vec3f IntegrateBRDF(Vec3f V, float roughness) {
const int sample_count = 1024;
float A = 0.0;
float B = 0.0;
Vec3f N = Vec3f(0.0, 0.0, 1.0);
for (int i = 0; i < sample_count; i++) {
Vec2f Xi = Hammersley(i, sample_count);
Vec3f H = ImportanceSampleGGX(Xi, N, roughness);
Vec3f L = normalize(H * 2.0f * dot(V, H) - V);
float NoL = std::max(L.z, 0.0f);
float NoH = std::max(H.z, 0.0f);
float VoH = std::max(dot(V, H), 0.0f);
float NoV = std::max(dot(N, V), 0.0f);
// TODO: To calculate (fr * ni) / p_o here - Bonus 1
float Fc = pow(1.0f - VoH, 5.0f);
float G = GeometrySmith(roughness, NoV, NoL);
float G_Vis = VoH * G / (NoV * NoH);
// //no split sum
// A += G_Vis;
// Split Sum - Bonus 2
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
// return { A / sample_count, A / sample_count, A / sample_count }; // No split sum version
return { A / sample_count, B / sample_count, 0.0 }; // Split sum
}Split Sum,该方法是对光照的剥离,我在上面章节有提到。但是作业要求有Split Sum的提高部分,我猜测应该是想让我们这样实现吧。但是仔细考虑的话其实也没必要这么实现,因为计算一次反射的能量,其Fresenl项为1即全反射,这里也不需要将F0剥离来使参数降维。就这样吧,这样得到的纹理如下:
Split Sum
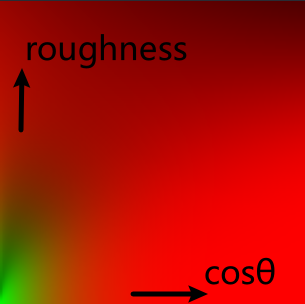
Not Split Sum
E_avg的预计算就比较简单了,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15Vec3f IntegrateEmu(Vec3f V, float roughness, float NdotV, Vec3f Ei) {
Vec3f Eavg = Vec3f(0.0f);
const int sample_count = 1024;
Vec3f N = Vec3f(0.0, 0.0, 1.0);
for (int i = 0; i < sample_count; i++) {
Vec2f Xi = Hammersley(i, sample_count);
Vec3f H = ImportanceSampleGGX(Xi, N, roughness);
Vec3f L = normalize(H * 2.0f * dot(V, H) - V);
float NoL = std::max(L.z, 0.0f);
// float pdf = 1;//跟roughness没关系
// TODO: To calculate Eavg here
Eavg += Ei * 2.0f * NoL ;//Ei * 2.0f * NoL, NoL : cos thetai
}
return Eavg / sample_count;
}
Split Sum

Not Split Sum

完成Kulla Conty Approximation
我们拿到已经预计算好的E(μ)和E_avg,现在就可以将新设计的BRDF积分值算出来了,代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19//split sum
vec3 MultiScatterBRDF(float NdotL, float NdotV, vec3 F)
{
vec3 albedo = pow(texture(uAlbedoMap, vTexCoords).rgb,vec3(2.2));
// A split-sum result in which R-channel repesent F interger term
vec3 E_o = texture(uKullaContyBrdflut, vec2(NdotL, uRoughness)).xyz;
vec3 E_i = texture(uKullaContyBrdflut, vec2(NdotV, uRoughness)).xyz;
// Split sum result add here.
vec3 Emu_o = F * E_o.x + vec3(1.0) * E_o.y;
vec3 Emu_i = F * E_i.x + vec3(1.0) * E_i.y;
vec3 E_avg = texture(uKullaContyEavglut, vec2(0, uRoughness)).xyz;
vec3 E_avgss = F * E_avg.x + vec3(1.0) * E_avg.y;
...
// TODO: To calculate fms and missing energy here
vec3 F_ms = (1.0 - Emu_o) * (1.0 - Emu_i) / (PI * (1.0 - E_avgss));
...
return F_ms;
}albedo为1情况下的能量。如果物体本身自带颜色,那还要考虑因为物体本身吸收能量而引起的能量损失。首先要定一个平均Fresenl项,来表示不同入射方向下打到微表面,平均被反射出去的能量占比多少。公式如下:
\[
\begin{align}
F_{avg}=\frac{\int_{0}^{1}F(\mu)\mu d\mu}{\int_{0}^{1}\mu d\mu} \\
=2\int_{0}^{1}F(\mu)\mu d\mu \tag{29}
\end{align}
\] 这篇论文中,给出了该公式硬编码下的代码:

其中r是albedo,入射角为0度时给的值。g是EdgeTint边缘色调,入射角为80度给的值。这篇文章教了我们怎么生成这两个值,我生成了金材质的R和G。R(0.94423,0.77611,0.37217),G(0.94806,0.86104,0.60760)。
有了平均Fresenl项,我们现在从新认识一下E_avg:含义为不考虑菲涅尔项时,不同入射角度打到微表面时,离开表面后平均能被你看到的能量。
那考虑上物体本身会吸收的颜色,我们能看到一次反射后的平均能量为\(F_{avg}E_{avg}\),则发生一次反射后没有出去的平均能量为\(F_{avg}(1-E_{avg})\),然后这部分能量再次发生反射后我们能看到的平均能量为\(F_{avg}(1-E_{avg})F_{avg}E_{avg}\),总结出K次反射后我们能看到的平均能量为\(F_{avg}^{k}(1-E_{avg})^{k}F_{avg}E_{avg}\),最后将这部分能量全部加起来,就是一个级数,其数学公式为:
\[
((F_{avg}(1-E_{avg}))^{0}+(F_{avg}^{}(1-E_{avg}))^{1}+(F_{avg}(1-E_{avg}))^{k})*F_{avg}E_{avg}
\tag{30}
\]
前面部分是一个等比数列,由于F_avg和1-E_avg都是小于1的数,所以结果为:
\[
=\frac{F_{avg}E_{avg}}{1-F_{avg}(1-E_{avg})} \tag{31}
\]
课堂上的讲解图片如下,需要注意的是这里的one bounce指的是两次反射:

这个公式就是颜色项,我们直接乘上之前没有考虑颜色时的能量补偿项,代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14vec3 MultiScatterBRDF(float NdotL, float NdotV)
{
vec3 albedo = pow(texture(uAlbedoMap, vTexCoords).rgb,vec3(2.2));
vec3 E_o = texture(uKullaContyBrdflut, vec2(NdotL, uRoughness)).xyz;
vec3 E_i = texture(uKullaContyBrdflut, vec2(NdotV, uRoughness)).xyz;
vec3 E_avg = texture(uKullaContyEavglut, vec2(0, uRoughness)).xyz;
//gold
vec3 edgetint = vec3(0.94806,0.86104,0.60760);
vec3 F_avg = AverageFresnel(albedo, edgetint);
// TODO: To calculate fms and missing energy here
vec3 F_ms = (1.0 - E_o) * (1.0 - E_i) / (PI * (1.0 - E_avg));
vec3 F_add = F_avg * E_avg / (1.0 - F_avg * (1.0 - E_avg));
return F_add * F_ms;
}
