Games101 Final Project
效果图
1024spp: Specular +
Glass(0.08 roughness) + Sliver(0.4
roughness)

1024spp: Specular + Glass(0.28
roughness)

1024spp: Diffuse + Glass(0.08
roughness)

不得不说,这镜面和透明材质一但引入,噪声就会变得非常大,本质上还是因为焦散或反射光的生成效率太低导致的,个人觉得需要用到Photon Mapping技术,以后有需要再来研究吧,没有镜面和透明材质,16ssp感觉还行:
16ssp Sliver(0.4 roughness) +
Gold(0.4 roughness)

下面是多重重要性采样(MIS)的结果:
16spp

源码
前言
这篇文章主要讲的是GAMES101的Next Event Estimation Path Tracing,以及BRDF,BSDF材质的编写,最后在此基础上实现了Multiple Importance Sampling,以提高收敛速度。路径追踪部分包含光线与三角形求交与隐式表面求交,加速结构的构建(BVH,SAH),光线与加速结构求交,以及全局光照的实现等。本文不讲的是框架理解,另外需要注意的是,在实现过程中一定一定要注意pdfValue等于0导致的NaN的情况,还有就是渲染方程中的cosθ记得限制在[0,1]之间,不然会得到意想不到的而且非常隐蔽的效果,排查起来很困难。
Whitted-Style Ray Tracing
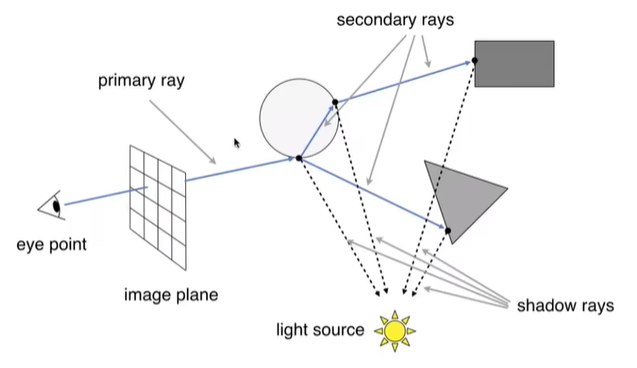
在介绍Path Tracing之前,我们先来看下Whitted-Style Ray Tracing:
 1.
对于屏幕上的每个像素我们都去打一根光线。
1.
对于屏幕上的每个像素我们都去打一根光线。
2.
发射出去的光线需要与场景中的物体进行求交,然后算光源对这个点的贡献(也可以使用Blinn
Phong算法),如果交点是玻璃材质的则产生反射光线和折射光线进行递归,直到光线打到Diffuse物体上。
3.
然后反向沿光线将交点处的颜色累加起来,期间经过了玻璃材质就按Fresnel项,算反射光线和折射光线的权重。
4. 最后将得到的颜色写入像素。
通过上面的步骤我们可以发现,如果光线打到是镜面,沿着它反射的方向获得的环境光还算是对的,因为Diffuse物体之间也会发生多次弹射。但是当光线打到Glossy物体上时,Whitted-Style Ray Tracing无法产生光线lobe,也就是说它只能沿着镜面反射采样,这样就无法得到下面右图的效果。

另一个问题是Whitted-Style Ray Tracing打到Diffuse物体就停住了,它不考虑该Diffuse物体受到环境的影响,这样就无法得到下面右图的效果。

还有最后一个问题,Whitted-Style Ray Tracing在计算光照对交点的影响时,以及反向沿光线将交点处的颜色累加起来时,都没有正确的考虑能量的传递过程,而Path Tracing为了解决这个问题,引入了辐射度量学的概念。
The Rendering Equation
对于辐射度量学,我们这里理清楚5个概念就行:
power(Radiant flux),\(\Phi=\frac{\text{d}Q}{\text{d}t}\)
即单位时间内的能量Solid Angle,\(\Omega=\frac{A}{r^2}\)
即球面上包含的某块面积比上距离平方:
Differential Solid Angles,\(\text{d}w=\frac{\text{d}A}{r^2}\)
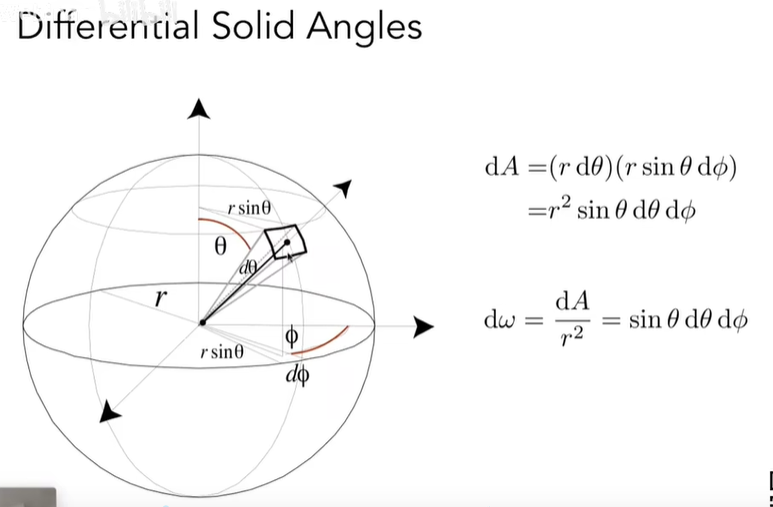
图中dA左边和右边的长度用弧长公式求得:rdθ
dA下面和上面的长度,先求水平面上的半径r sinθ,再利用弧长公式求得:r sinθ dφ,则dw为:
\[ \begin{align} \text{d}w=\frac{\text{d}A}{r^2}=\sin\theta\text{d}\theta\text{d}\phi \end{align} \tag{1} \]Irradiance,\(E(x)=\frac{\text{d}\Phi(x)}{\text{d}A}\)
即单位面积上接收到或辐射出的能量:

如果面积和光源不是正对着,还要乘上一个cosθ。Radiance,\(L(p,w)=\frac{\text{d}^2\Phi(p,w)}{\text{d}w\text{d}A\cos\theta}\)
即单位面积上并且在单位立体角上的能量,可以是接受到的也可以是辐射出的。
通过上面两者的准确定义,我们可以得到Irradiance和Radiance的关系:
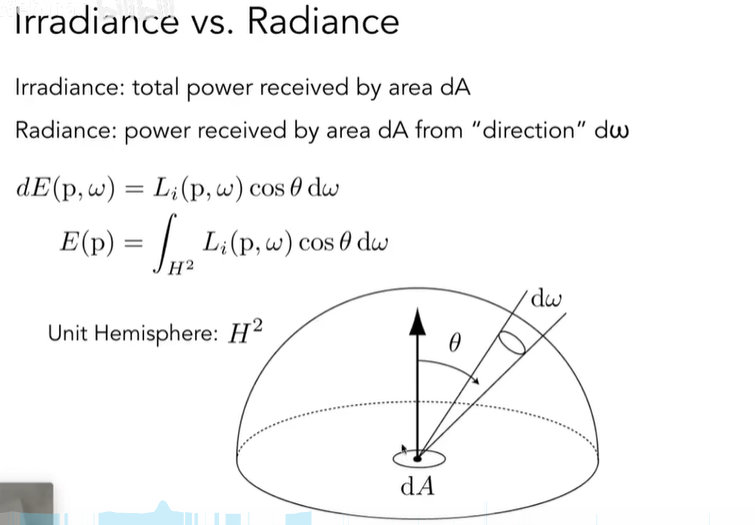
假设这是Incident Radiance,则Irradiance就是各个方向上接受到的能量总和,积分就是求和,是一样的意思。假设只有一个方向上能接收到光照的能量,则dA对应的Irradiance和dA从这个方向上来的能量(Radiance
* cosθ * dw)是相等的。
下面我们来理解一下,反射是什么。可以这样认为,反射是入射方向来的Radiance,转换成Irradiance后,最后再向出射方向辐射出的Radiance:
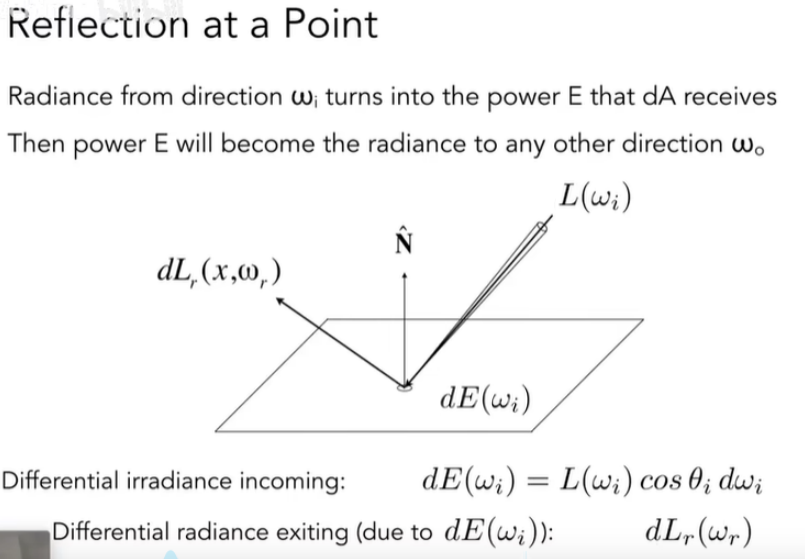
现在我们知道反射最后得到的是dA对应的Irradiance向反射方向辐射出的Radiance,但是我们不知道的是这个辐射出的Radiance和dA对应的Irradiance之间的关系,如果有一个函数可以描述这种行为那问题就解决了。
而BRDF(双向反射分布函数),就可以描述dA对应的Irradiance向某反射方向辐射出Radiance具体是多少:
\[
\begin{align}
\text{d}L_r(w_r)=f_r(w_i,w_r)\cdot\text{d}E_i(w_i)
\end{align} \tag{2}
\] 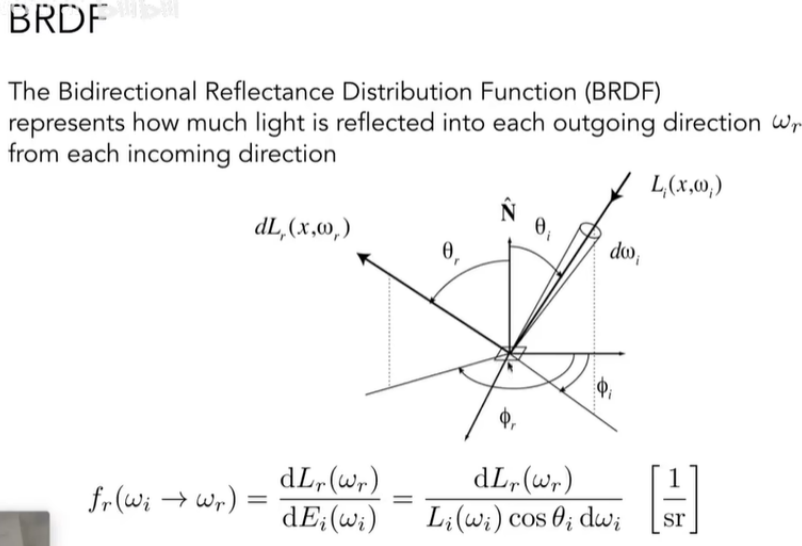
最后我们吧\(\text{d}E_i(w_i)\)换成Radiance的形式得到下面方程:
\[
\begin{align}
\text{d}L_r(w_r)=f_r(w_i,w_r)\cdot L_i(w_i)\cos\theta\text{d}w_i
\end{align} \tag{3}
\]
现在只是某一个入射方向w_i对出射方向w_r的贡献,然后两边分别积分得到出射方向w_r总共的Radiance:
\[
\begin{align}
L_r(w_r)=\int_{\Omega+}f_r(w_i,w_r)\cdot L_i(w_i)\cos\theta\text{d}w_i
\end{align} \tag{4}
\] 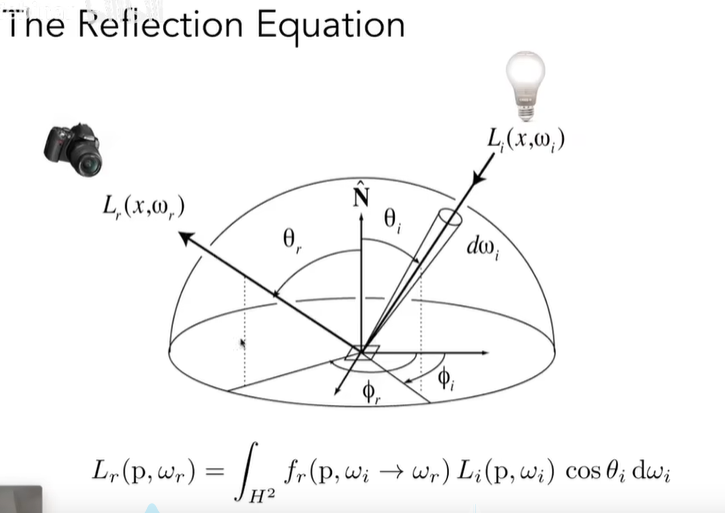
这就是反射方程的由来。而渲染方程就是在这基础上加上了一个自发光项:
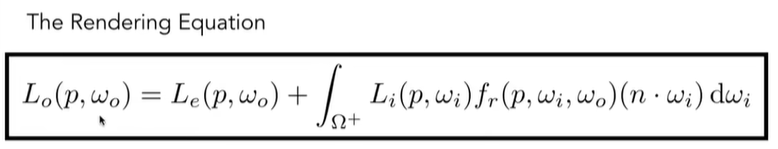
NEE Path Tracing
我们看图15,可以发现Le,BRDF,cosθ我们已经知道了,剩下的就是Li。而Li并不是只来自光源,还来自它周围的间接光(其他物体被照亮后也算是一个小型光源)。这样对于我们看到一个物体表面,它的Li,即要考虑直接光对它的影响,又要考虑间接光对它的影响。而间接光又得继续考虑直接光和间接光。从而形成一个递归过程(NEE
Path Tracing):
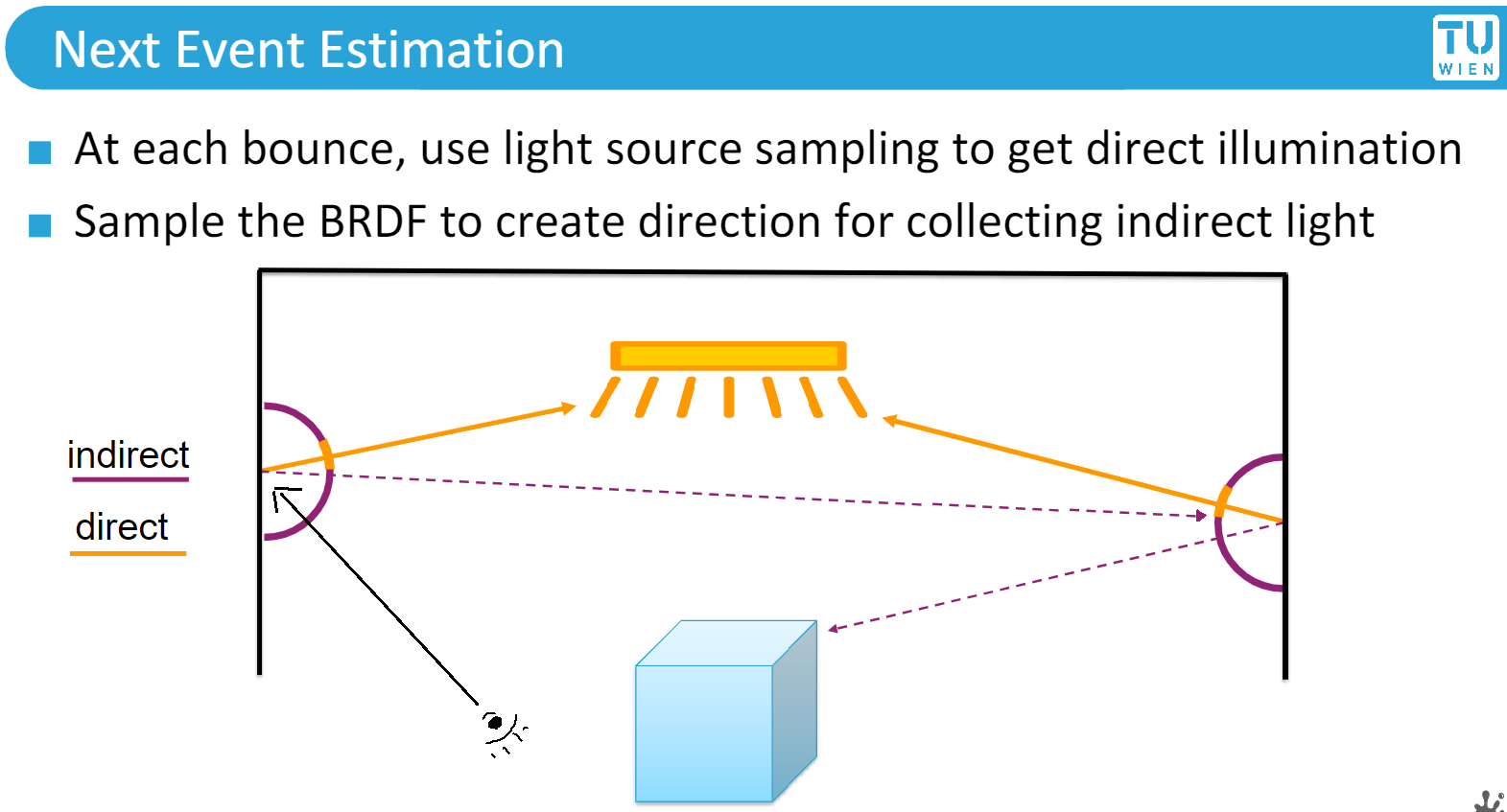
下面是这一递归过程的伪代码:

这里用到了Russian Roulette的概念,因为间接光不能一直递归下去,而我们又想得到的期望值不变,假设期望值为Lo。我们均匀的取一个随机变量P(0
< P <
1),以P概率进行递归,1-P的概率毙掉这根光线,则离散型随机变量的期望为:
\[
\begin{align}
E(X)=P*L_o+(1-P)*0
\end{align} \tag{5}
\]
为了其期望值最后还是Lo,我们只需要将得到的间接光Lo除以P就行:
\[
\begin{align}
E(X)=P*(\frac{L_o}{P})+(1-P)*0=L_o
\end{align} \tag{6}
\]
Monte Carlo Integral
上面伪代码中,没有说渲染方程(不考虑自发光)在代码中应该怎么实现,对于一个定积分我们可以用蒙特卡洛的方法来近似求解这个积分:

在积分域上,用任意一种概率密度函数(PDF),去采样多个位置Xi,则该定积分的值为:
\[
\begin{align}
F_N=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}
\end{align} \tag{7}
\]
如果是均匀的采样一个位置,则PDF就是一个常值:
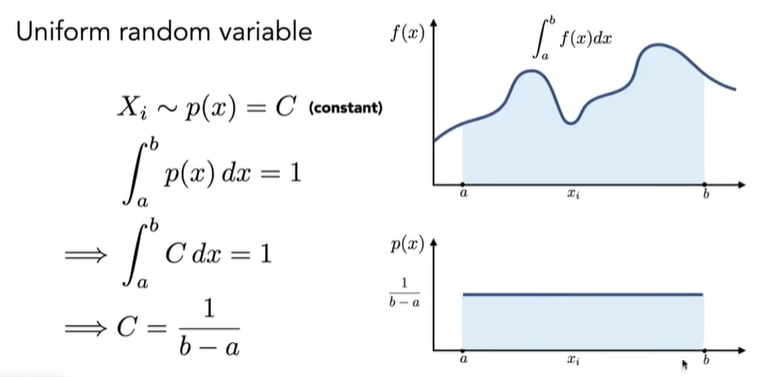
7式可以写成:
\[
\begin{align}
F_N=\frac{b-a}{N}\sum_{i=1}^{N}f(X_i)
\end{align} \tag{8}
\]
但是我们一般不会去用均匀采样,因为噪声很大。如果有一个PDF,其形状和f(x)大致吻合,那么用这样的PDF去采样一个位置或方向,收敛速度更快,这就是重要性采样(我在这篇文章中有详细讲到重要性采样的过程)。
渲染方程写成蒙特卡洛积分的形式如下:
\[
\begin{align}
L_o(p,w_o)=\int_{\Omega+}L_i(p,w_i)f_r(p,w_i,w_o)(n\cdot w_i)\text{d}w_i
\\
\approx\frac{1}{N}\sum_{i=1}^{N}\frac{L_i(p,w_i)f_r(p,w_i,w_o)(n\cdot
w_i)}{p(w_i)}
\end{align} \tag{9}
\]
但是如果每个交点都向外发射N条光线,指数爆炸还是吃不消:
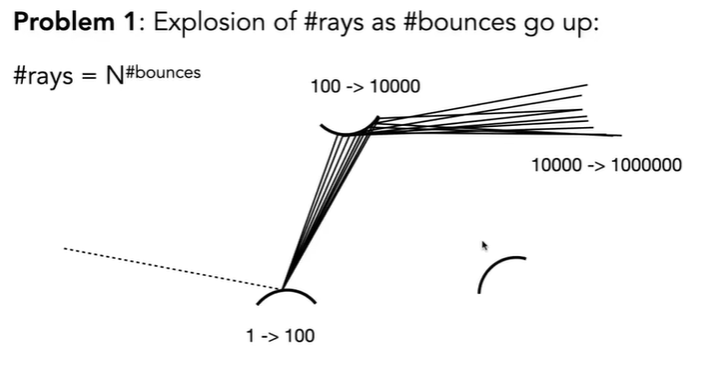
我们就让交点每次只产生一条光线向外追踪,然后在一个像素里面多打几条光线,这样就可以避免指数爆炸:
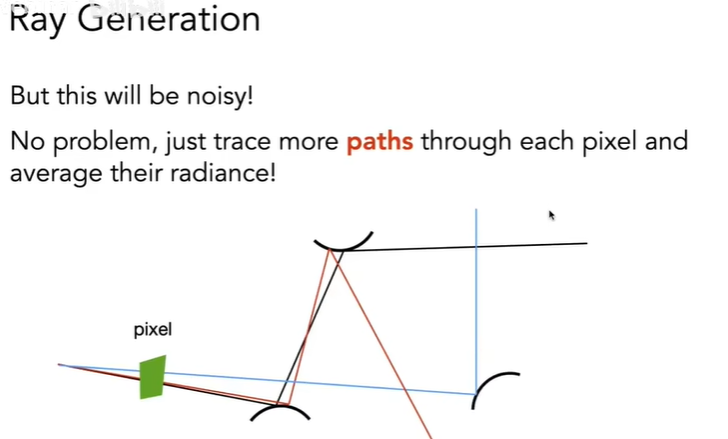
下面是更新后的NEE Path Tracing伪代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19function Li(p,wo,depth)
if(depth==0 && Ray hit light source)
return LightRadiance;
P_RR = 0.8;
Randomly select ksi in a uniform dist. in [0,1]
if(ksi > P_RR) return 0.0;
Randomly select a sampling point on the light source, p_on_light
Trace a shadowRay sr(p,(p_on_light - p).normalized() )
if(ray sr does not hit an object except light source)
direct = LightRadiance * f_r * cosθ / pdfLight_solidAngle;
Randomly choose One direction wi ~ pdf(w)
Trace a ray r(p,wi)
if(ray r hit an object at q && does not hit light source)
indirect = Li(q,-wi,depth+1) * f_r * cosθ / pdf(wi);
return (direct + indirect) / P_RR;Trace函数,在Trace光线时,我们需要判断光线与场景中物体的求交,而场景中大部分的物体都是由三角形组成的,所以我们需要一个高效的算法来判断光线与三角形求交。
光线与三角形求交
要想求光线是否与三角形相交,我们很自然可以想到一种方法,先判断光线与三角形所在的平面是否相交,然后再判断交点是否在三角形内。

我们定义一个射线方程:\(r(t)=o+t*\vec d,0\leq
t<\inf\),再定义一个平面方程: \((p-p')\cdot\vec
N=0\),然后假设p等于r(t)则我们可以求出t这个系数:
\[
\begin{align}
& (p-p')\cdot\vec N=(o+t*\vec d-p')=0 \\
& t=\frac{(p'-o)\cdot\vec N}{\vec d\cdot N}
\end{align} \tag{10}
\]
判断点在三角形内,直接将交点p与三角形各个顶点按顺序相连,假设是逆时针,连到第一个顶点得到的向量与第一个顶点和第二顶点的向量做叉乘,转一圈,然后判断叉乘出的方向是否同向,同向在三角形里面,不同向则不在。
这种方法可以用来判断求交,但是效率不高,有一个效率更高的算法Moller Trumbore,它是一种可以快速求解直线与三角形求交的算法,通过三阶方阵行列式的混合积可以快速得出交点与重心坐标,然后判断重心坐标是否大于零,且1-u-v也要大于零。要推导它还比较麻烦,需要用到混合积和克莱姆法则。
先介绍一下混合积的快速记忆法:
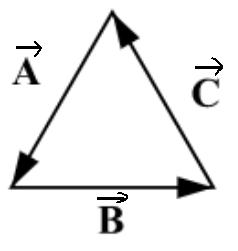
对于一个三阶方阵的行列式:
\[
\begin{align}
\left | \begin{matrix}
A_1 & B_1 & C_1 \\
A_2 & B_2 & C_2 \\
A_3 & B_3 & C_3
\end{matrix} \right |
\end{align} \tag{11}
\] 其混合积可以写成以下形式:
\[
\begin{align}
(\vec A\times\vec B)\cdot\vec C=(\vec B\times\vec C)\cdot\vec A=(\vec
C\times\vec A)\cdot\vec B
\end{align} \tag{12}
\] 克莱姆法则:
对于线性方程组 \(A\vec x = \vec c\),
其中A是可逆方阵,\(\vec x,\vec
c\)都是列向量,那么方程有解,且\(\vec
x\)的每一个解为:
\[
\begin{align}
x_i=\frac{\text{det}A_i}{\text{det}A}
\end{align} \tag{13}
\] 其中A_i是被列向量\(\vec
c\)取代了第i列的矩阵。
下面是MT算法的推理,如下:
三角形中的某一点可以写成重心坐标的形式,该点也可以由射线方程得到,则可以得到下面等式:
\[
\begin{align}
O+t*\vec D=(1-u-v)*\vec V_0+u*\vec V_1+v*\vec V_2 \\
O-\vec V_0=(\vec V_1-\vec V_0)*u+(\vec V_2-\vec V_0)*v-t*\vec D
\end{align} \tag{14}
\] 设:
\[
\begin{align}
& \vec S=O-\vec V_0 \\
& \vec E_1=\vec V_1-\vec V_0 \\
& \vec E_2=\vec V_2-\vec V_0 \\
\\
& \vec S=\vec E_1*u+\vec E_2v-t*\vec D
\end{align} \tag{15}
\] 这是一个线性方程组,我们可以写成如下形式:
\[
\begin{align}
[-\vec D,\vec E_1,\vec E_2]\cdot
\left[\begin{matrix}
t\\
u\\
v
\end{matrix} \right]
=\vec S
\end{align} \tag{16}
\] 由克莱姆法则得到它们的解为:
\[
\begin{align}
t=\frac{\text{det}(\vec S,\vec E_1,\vec E_2)}{\text{det}(-\vec D,\vec
E_1,\vec E_2)} \\
u=\frac{\text{det}(-\vec D,\vec S,\vec E_2)}{\text{det}(-\vec D,\vec
E_1,\vec E_2)} \\
v=\frac{\text{det}(-\vec D,\vec E_1,\vec S)}{\text{det}(-\vec D,\vec
E_1,\vec E_2)}
\end{align} \tag{17}
\] 再由混合积可得到分母和分子行列式的值:
\[
\begin{align}
& \text{det}(-\vec D,\vec E_1,\vec E_2)=-\vec D\cdot (\vec
E_1\times\vec E_2)=\vec E_1\cdot(\vec E_2\times-\vec D)=\vec
E_1\cdot(\vec D\times\vec E_2)=\vec E_1\cdot\vec S_1 \\
& \text{det}(\vec S,\vec E_1,\vec E_2)=\vec S\cdot (\vec
E_1\times\vec E_2)=\vec E_2\cdot(\vec S\times\vec E_1)=\vec E_2\cdot\vec
S_2 \\
& \text{det}(-\vec D,\vec S,\vec E_2)=-\vec D\cdot (\vec S\times\vec
E_2)=\vec S\cdot(\vec D\times\vec E_2)=\vec S\cdot\vec S_1 \\
& \text{det}(-\vec D,\vec E_1,\vec S)=-\vec D\cdot (\vec
E_1\times\vec S)=\vec D\cdot(\vec S\times\vec E_1)=\vec D\cdot\vec S_2
\end{align} \tag{18}
\] 则:
\[
\begin{align}
t=\frac{\vec E_2\cdot\vec S_2}{\vec E_1\cdot\vec S_1} \\
u=\frac{\vec S\cdot\vec S_1}{\vec E_1\cdot\vec S_1} \\
v=\frac{\vec D\cdot\vec S_2}{\vec E_1\cdot\vec S_1}
\end{align} \tag{19}
\] 这就是课堂上看到的公式:
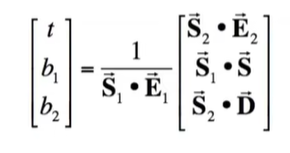
光线与隐式表面求交
这里举一个最简单的例子,光线与球面求交,其过程和上面光线与平面求交类似:
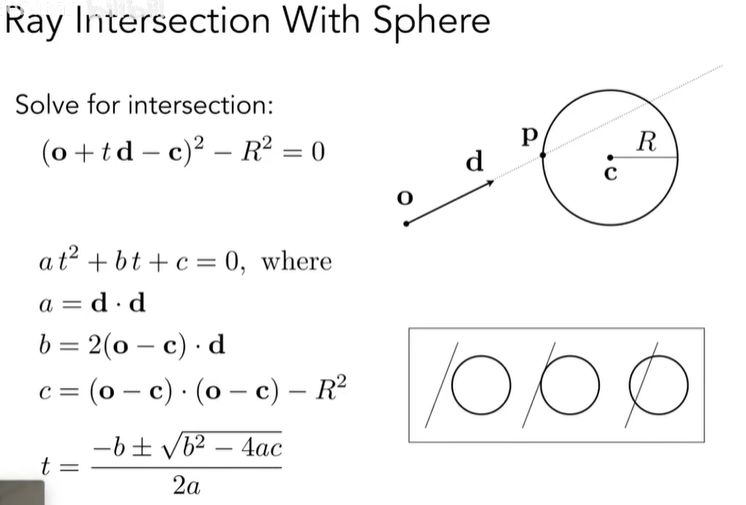
还是一样用射线方程代替球面上一点P,然后直接求二次函数的根。
加速结构Bounding Volume Hierarchy
有了MT算法,我们可以很快判断光线是否与三角形相交,而隐式表面的求交也很快。但复杂场景中的三角形面数非常多,如果每次光线弹射一次都要与场景中所有三角形求交,计算量还是太大了,不过我们可以构建一个加速结构BVH,来解决这个问题,在此之前先介绍一下
Bounding Volume是什么东西:

我们可以用一个简单的包围盒包住一个复杂的物体,先对包围盒求交再对复杂物体求交,这样当光线没有与包围盒相交时,就可以避免与复杂物体求交,这可以节省大量时间。
在三维场景中,包围盒通常是横平竖直的轴对齐包围盒(AABB):
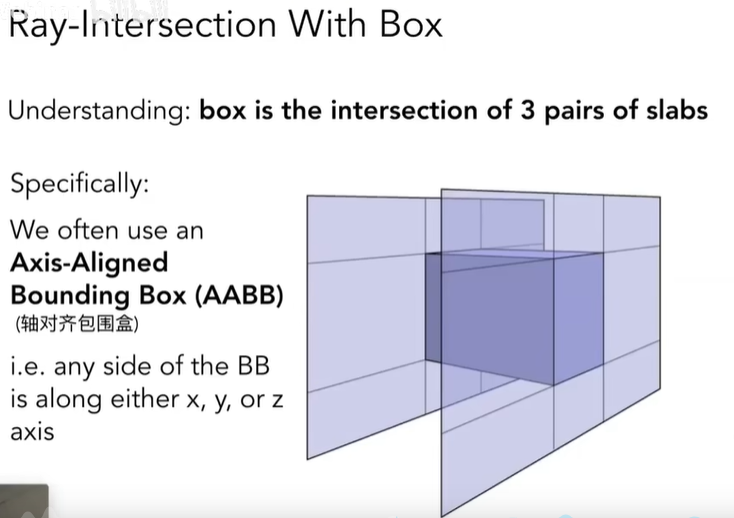
这种包围盒有个特点,它的平面都是xy yz
zx平面,没有任何旋转,分别和z x
y轴垂直,这样我们就可以降维处理每一对平面,然后利用下面公式计算光线进入和出去这对平面的时间,这里假设是yz平面:
\[
\begin{align}
& t_{min}=\frac{X_0-O}{\vec {d}.x} \\
& t_{max}=\frac{X_1-O}{\vec {d}.x}
\end{align} \tag{20}
\] 其他对平面的处理方式相同:
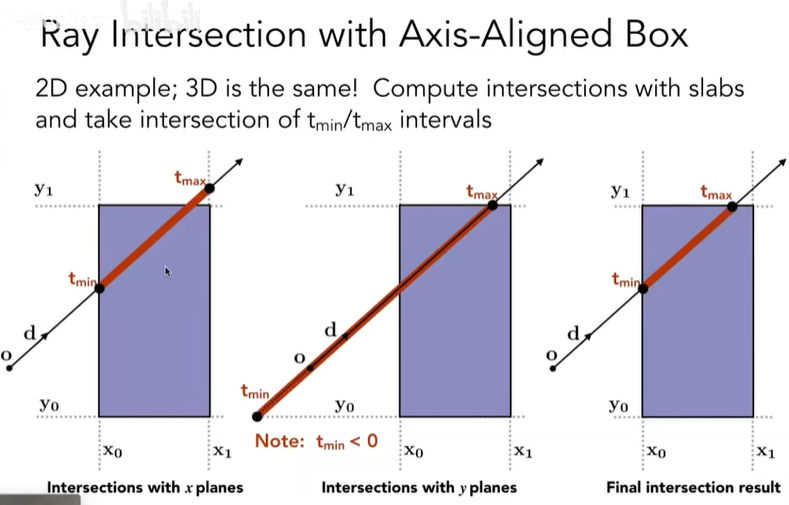
从图中可以看出来,t_min要的是三对平面中最大的一个,而t_max则要的是三对平面中最小的一个,所以我们用下面公式来求得光线进入t_enter包围盒以及出去t_exit包围盒的时间:
\[
\begin{align}
& t_{enter}=\text{max}(t_{min})\\
& t_{exit}=\text{min}(t_{max})
\end{align} \tag{21}
\] 最后我们判断一下什么情况下,光线会与包围盒相交:
1.
t_enter < t_exit,这种情况说明光线在包围盒中停留了一段时间,所以是相交。
2.
t_enter < 0 && t_exit >=0,这说明光线就在包围盒内部,那肯定是相交。
综合这两种情况得光线与包围盒相交的条件t_enter < t_exit && t_exit >=0。
现在有了包围盒,但是光线和包围盒相交后,如果物体很复杂,那还是要和物体上每个三角形求交,只用一个包围盒还是达不到我们预期,我们需要构建一个加速结构,然后将复杂物体的三角形不断划分到子包围盒中,这里介绍两种划分方法:
第一种是空间划分法,以KD-Tree为例:
对空间进行二分(一般是取中间进行划分),每个父节点都有两个子节点,为了保证场景划分的均匀,每次都会沿着xyz轴划分,上次是沿x轴则下次就是y轴,再下次就是z轴,如此循环,直到叶子节点包含的三角形数量比较少时停止划分,其中非叶子节点不存储三角形:

有了这个加速结构,我们再Trace一个物体时,就能有效避免和整个物体的三角形求交,时间复杂度由\(O(n)\)降为\(O(\log_{2}n)\):
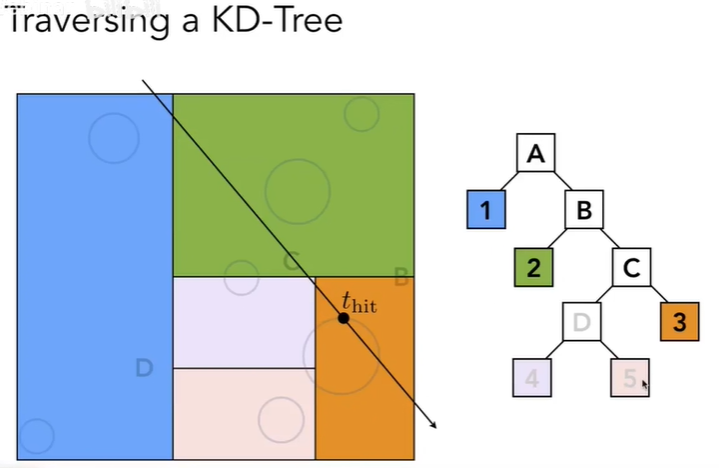
图中蓝色块和A的子节点一样处理,只不过这里隐藏了。
但是空间划分有个严重的问题,三角形会和包围盒相交,我们得知道包围盒和哪些三角形有交集,才能将这些三角形存储到叶子节点中,这样问题又变得比较复杂了,所以我们一般不用KD-Tree来划分空间,而是用BVH来划分物体,从而避免判断三角形和包围盒求交的问题。
第二种方法则是物体划分法,以BVH为例,现在基本上只要是跟光线追踪有关的加速结构,都是用的类似BVH来解决的,可见其重要性。
BVH的划分思路和KD-Tree是类似的,即对物体的三角形进行二分(后面说具体的划分法),然后分别求子节点的包围盒,非叶子节点也是一样不存储三角形只用于判断是否相交,叶子节点在包围盒内三角形比较少时停止划分:
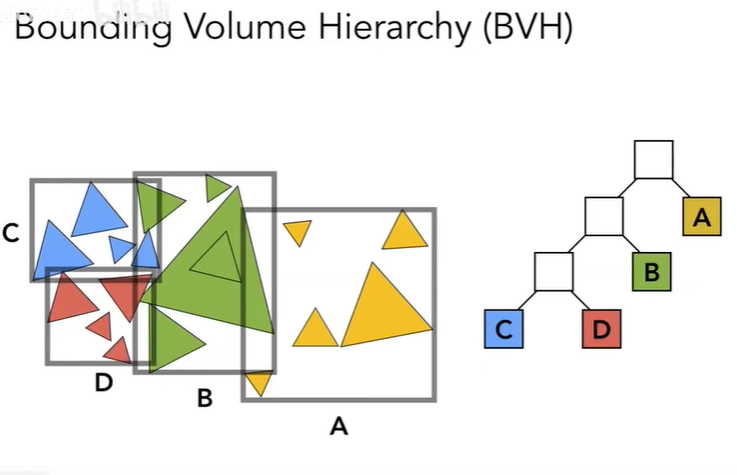
用BVH划分也会有点小问题,那就是包围盒重叠,重叠部分越多需要访问的节点数量就越多,求交的效率就越低,我们需要一个好的方法去尽量避免重叠,一个还算不错且比较通用的手段是对物体先进行排序,然后取中间物体作为分割线,在此之前还要向KD-Tree学习,我们找到当前节点下能包围所有三角形的包围盒,获取包围盒的pMAX-pMin向量,然后判断该向量的xyz分量,取最大分量的轴为排序轴:

需要注意的是我上面说的分别求子节点的包围盒这过程是在回溯过程中完成的,递归完成的是排序和划分,为了限制文章长度,就不贴代码了。
相比于BVH,还有一个更加高效的方法Surface Area Heuristic:
我们先来看下这个例子:
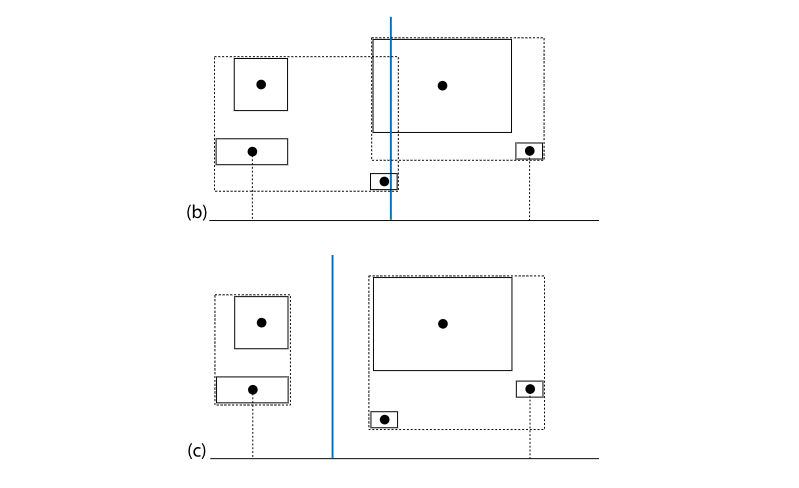
假设我们已经对图b和图c在某轴上排序好了他们的包围盒,按照BVH的划分思路,它划分好的样子是图b,但是很明显图c是个更好的选择,而SAH就可以做这样的一件事情。
正如它的名字所说,这个算法考虑了包围盒的表面积,不再是中间一刀切。具体来说,它将包围盒分成了若干个桶,就下图而言,有6个桶:
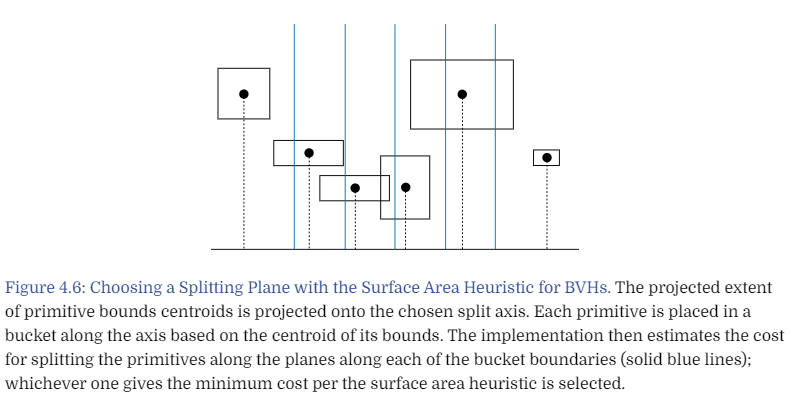
然后记录每个桶中三角形的数量,并依次按桶的边界对包围盒进行二分,然后记录每次分割后的开销,用下面这个公式计算:
\[
\text{cost}(A,B)=t_{trav}+p_A\sum_{i=1}^{N_A}t_{isect}(a_i)+p_B\sum_{i=1}^{N_B}t_{isect}(b_i)
\tag{22}
\] 其中A,B是分割后的两个包围盒。
t_trav代表访问该节点的开销,不是求交,就是单纯的获取数据读取数据,我们一般把它设为0.125。
t_isect(a_i)代表对包围盒A内的某个三角形求交的开销,我们一般将其设为1,t_isect(b_i)同理。
对于p_A和p_B,看下面图例:
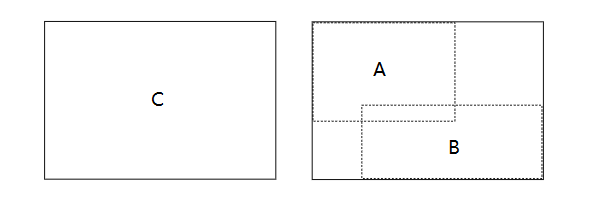
光线穿过包围盒C的前提下穿过包围盒A的概率为\(p_A=\frac{S(A)}{S(C)}\),同理\(p_B=\frac{S(B)}{S(C)}\),其中S(x)函数的作用为获取包围盒的表面积。
这样上面22式就可以简化为:
\[
\begin{align}
\text{cost}(A,B)=0.125+\frac{S(A)}{S(C)}*N_A+\frac{S(B)}{S(C)}*N_B
\end{align} \tag{23}
\]
最后选择开销最小的分割线对物体进行分割,递归下去,直到包围盒内三角形数量较少时停止。这部分的代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86double BVHAccel::computeObjSurArea(const std::vector<Object *>& objects){
double area = 0;
for(const auto& obj:objects){
area += obj->getBounds().SurfaceArea();
}
return area;
}
BVHBuildNode * BVHAccel::recursiveBuildSAH(std::vector<Object *> objects){
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
node->area = objects[0]->getArea();
return node;
}
else if (objects.size() == 2) {
node->left = recursiveBuildSAH({objects[0]});
node->right = recursiveBuildSAH({objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
node->area = node->left->area + node->right->area;
return node;
}
else {
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
double boundsSurfaceAreaInv = 1.0f / bounds.SurfaceArea();
auto beginning=objects.begin();
auto ending=objects.end();
if(objects.size() < 4){
auto middling = objects.begin() +objects.size()/2;
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
node->left = recursiveBuildSAH(std::move(leftshapes));
node->right = recursiveBuildSAH(std::move(rightshapes));
node->bounds = Union(node->left->bounds, node->right->bounds);
node->area = node->left->area + node->right->area;
}
else {
int bestChoice=0;
double minCost=std::numeric_limits<double >::max();
double objSize =(double)objects.size();
double nums[]={1.0/12,2.0/12,3.0/12,4.0/12,5.0/12,6.0/12,7.0/12,8.0/12,9.0/12,10.0/12,11.0/12};
for(int i = 0;i < 11;i++)
nums[i]*= objSize;
int dim = bounds.maxExtent();
switch (dim){
case 0://x
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2)
{ return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x; });
break;
...//y z
}
for(int i = 0;i < 11;i++){
auto middling = objects.begin() + (int)nums[i];
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
double leftBoxArea = computeObjSurArea(leftshapes);
double rightBoxArea = computeObjSurArea(rightshapes);
double cost = 0.125f+
( leftBoxArea * leftshapes.size() + rightBoxArea * rightshapes.size() )
* boundsSurfaceAreaInv;
if(cost < minCost){
minCost = cost;
bestChoice=(int)nums[i];
}
}
auto middling = objects.begin() + bestChoice;
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
node->left = recursiveBuildSAH(std::move(leftshapes));
node->right = recursiveBuildSAH(std::move(rightshapes));
node->bounds = Union(node->left->bounds, node->right->bounds);
node->area = node->left->area + node->right->area;
}
return node;
}
}BVH的对比效果图如下:
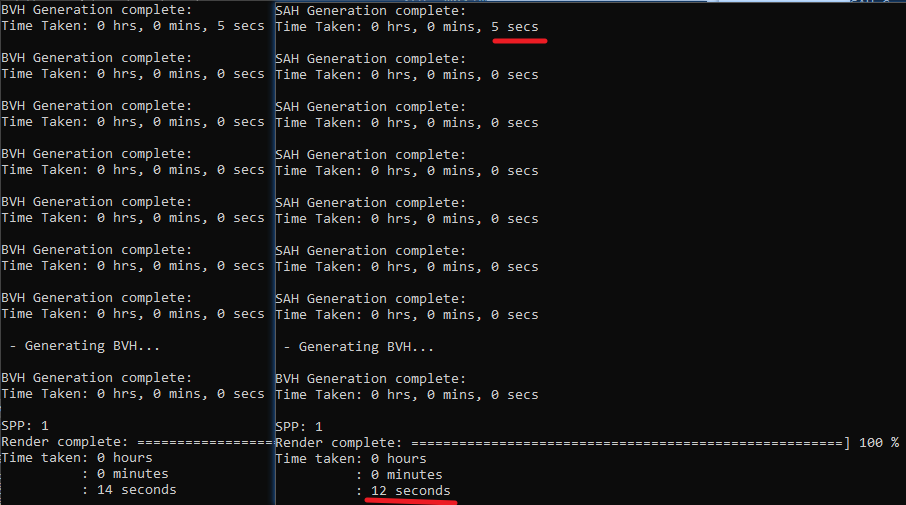

快了一点点,不多,可能在更复杂的场景下差距会拉开。
上面部分图片来源于pbrt-SAH。
直接光采样
回到NEE Path Tracing:
1
2
3
4
5
6
7function Li(p,wo,depth)
...
Randomly select a sampling point on the light source, p_on_light
Trace a shadowRay sr(p,(p_on_light - p).normalized() )
if(ray sr does not hit an object except light source)
direct = LightRadiance * f_r * cosθ / pdfLight_solidAngle;
...pdfLight_solidAngle我们还不知道怎么算。但是我们知道BRDF采样,用一种概率密度函数(PDF),去采样一个方向wi,并且获得该方向的pdf是多少,下面是cos weight PDF得到的16spp直接光采样效果:

这效果太差了,因为BRDF采样对于Diffuse物体而言,它很难生成一根打中光源的光线,我们要改进这一点,让物体直接对光源采样:
对光源的采样主要是获得采样方向wi以及它的pdf,我们可以在面光源上随机选择一个采样点,对于物体上的一点x与它连线,形成ShadowRay,因为是在光源上随机选择一个采样点,所以采样光源的pdf为1/A,A为光源的面积,再将渲染方程对dw的积分换成dA的积分即可:

但是我不这样做,因为后面多重重要性采样需要pdf在同一个角度考虑,要么是在立体角上要么是在面积上,而我选择的是立体角上,即将光源的面积投影到立体角上,然后获得光源在立体角上的pdf,其过程和上面dw转换为dA类似:
\[
\begin{align}
pdfLight\text{-}SolidAngle=\frac{A\cos\theta'}{||x-x'||^2}
\end{align} \tag{24}
\] 代码中渲染方程还是写成下面这种形式:
1
Le += L_dir_Inter.emit * f_r * std::fmax(dotProduct(w_Li, intersection.normal),0.0) / light_solidAngle_pdf;1spp直接光采样的效果:

可以看到这比16sppBRDF采样的效果好太多!而间接光如何处理在上面伪代码中已经写出来,这部分没有什么特别的,我们看16spp全局光照的效果:

还是挺不错的😆!代码就不贴了,可以看下我的源码,有详细注释!
BRDF and BSDF
BRDF
BRDF这个R指的是反射,而BSDF的S指的是散射,它由BRDF和BTDF组成的,先来看下BRDF,我们一般用的是Cook-Torrance反射方程:
\[
\begin{align}
L_{o}(p,w_{o})=\int_{\Omega}^{}(kd\frac{c}{\pi}+ks\frac{DFG}{4(w_{o}\cdot
n)(w_{i}\cdot n)})L_{i}(p,w_{i})n\cdot w_{i}dw_{i}
\end{align} \tag{25}
\]
因为这里ks和Fresnel项指代的是同一个东西,我们可以去掉ks,其中o代表出射方向也就是我们看到的方向,i是入射方向即光照方向。
这个方程的推导就不细说了,其实我也没推过😑,能用就行哈哈,不过它的作用我在上文中已经详细讲过了,可以去看下。说下这里每项具体都是些什么东西:
kd表示折射或漫反射部分所占的比例,而ks则是反射比例。在BRDF中kd就是漫反射部分kd=1.0-ks。因为金属不会折射光线,因此不会有漫反射,如果表面是金属的,我们会把系数kd变为0,即kd=(1.0-ks)*(1.0-metallic)。
c/π是兰伯特项,也称作Diffuse项,c是albedo,除以π是为了能量守恒,上面我有提到BRDF的定义是入射光的Irradiance向反射方向wo辐射出的Radiance是多少,也就是它们的比率,假设漫反射辐射出的能量是c,入射光的Radiance为1,因为漫反射的BRDF是常值则有下面等式:
\[
\begin{align}
& c=f_r\int_{\Omega+}\cos\theta\text{d}w_i \\
& c=f_r*2\pi*\int_{0}^{\frac{\pi}{2}}\sin\theta\text{d}\sin\theta \\
& c=f_r*2\pi*\frac{\sin^2\theta}{2}|_{0}^{\frac{\pi}{2}}\\
& c=f_r*\pi\\
& f_r=\frac{c}{\pi}
\end{align} \tag{26}
\]
\(\frac{DFG}{4(w_{o}\cdot n)(w_{i}\cdot
n)}\)这坨东西是Specular反射项。它是基于微平面理论推导出来的,微平面理论假设物体是由很多微平面组成,每个微平面都是绝对光滑的,但是都非常小,没办法一个一个观察到,只能看到统计后的宏观结果。它下面\(4(w_{o}\cdot n)(w_{i}\cdot
n)\)是一个校正因子,用来校正从微平面的局部空间转到整体表面时的数量差异。
Normal Distribution Function
D项为GGX法线分布函数,Glossy物体采样某方向的PDF函数就是由该函数乘上cos在半球积分所得:
\[
\begin{align}
\int_{\Omega+}D(h)(n\cdot h)\text{d}w_h=1
\end{align} \tag{27}
\] 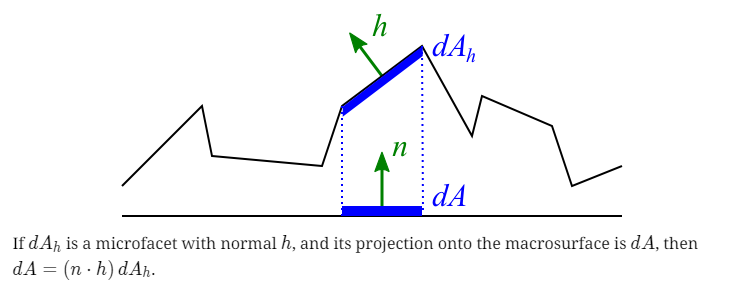
乘上cos项是为了将微平面投影到立体角上,n是表面的法线,h是半程向量。关于这里cos的来源更多内容看这篇文章。有了概率密度函数,根据逆变换采样就可以得到具体的方向了,我在这篇文章有详细讲到逆变换采样和重要性采样怎么算。
看下D项具体的作用以及函数式:
\[
\begin{align}
NDF_{GGX}(n,h,\alpha)=\frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2-1)+1)^2}
\end{align} \tag{28}
\]
其中α是粗糙度,n是宏观表面法线,h是半程向量。该函数D(h)描述了半程向量h和微平面法线的分布关系,其取值范围如下:
\[
\begin{align}
0\leq D(h)\leq \infty
\end{align} \tag{29}
\]
该函数是用来控制Specular高光的大小,亮度和形状,α越大粗糙度越大,半程向量h和微表面法线一致的范围变大,但是光斑强度会减弱:

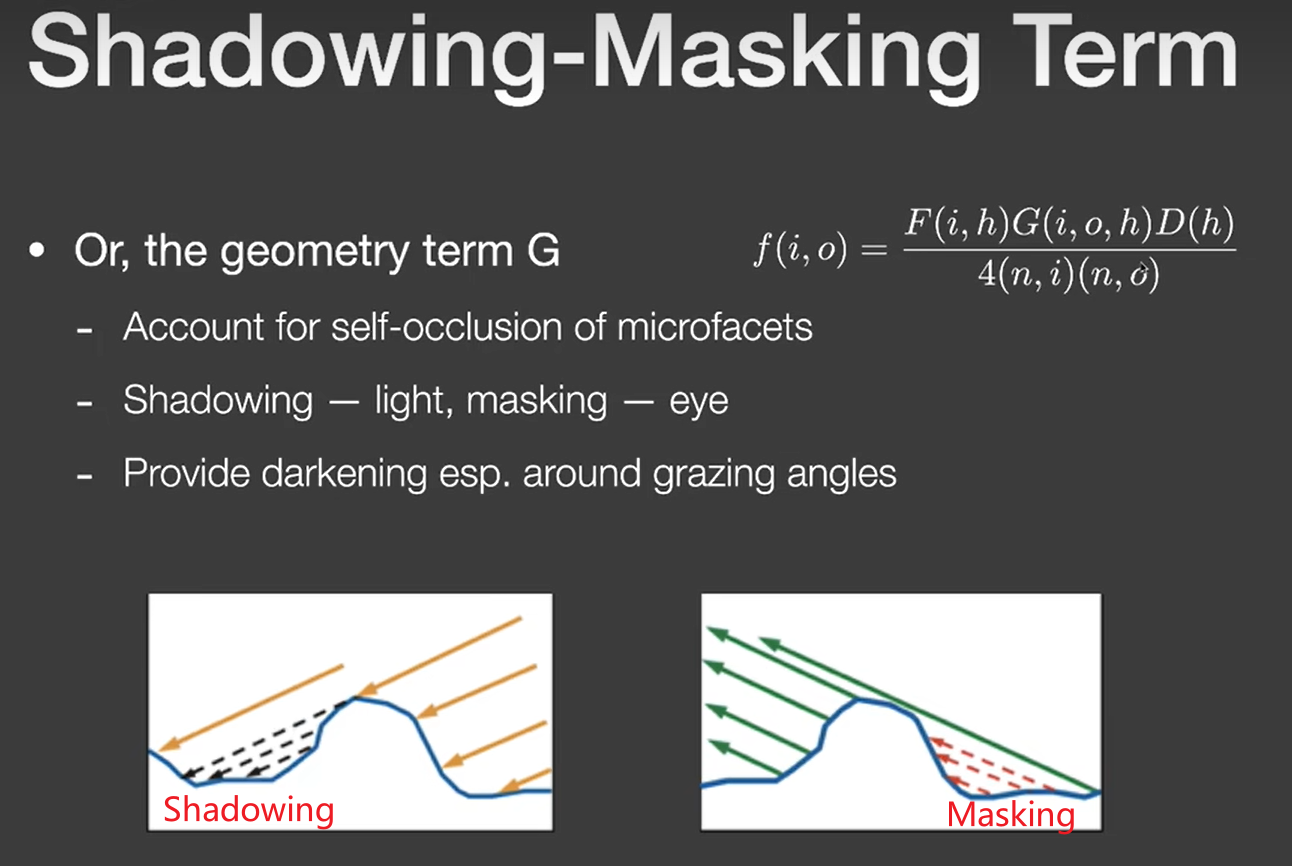
Shadowing Masking Function
G是几何项,而G项包含了Shadowing和Masking两项,为了简化操作,我们通常用\(G_{Schlick\text{-}GGX}\)来计算这两项的值:
\[
\begin{align}
G(n,v,l,k)=G_{Schlick\text{-}GGX}(n,v,k)G_{Schlick\text{-}GGX}(n,l,k)
\end{align} \tag{30}
\]
Schlick-GGX几何函数是GGX与Schlick-Beckmann近似的结合体:
\[
\begin{align}
G_{Schlick\text{-}GGX}(n,v,k)=\frac{n\cdot v}{(n\cdot v)(1-k)+k}
\end{align} \tag{31}
\]
其中n是宏观表面法线,v是入射方向或者出射方向,而k是粗糙度α的重映射形式,k的计算取决于我们针对直接光照还是IBL光照:
\[
\begin{align}
k_{direct}=\frac{(\alpha+1)^2}{8} \\
k_{IBL}=\frac{\alpha^2}{2}
\end{align} \tag{32}
\]
该函数是用来描述由于微表面自遮挡产生的变暗现象。因为微表面的自遮挡现象,以至于得到的结果不如我们计算出来结果那么亮。
Shadowing是光打到微表面时,由于微表面的自遮挡现象而导致一部分微表面未能接受到光照。
Masking则是光打到微表面后,由于微表面的自遮挡现象一部分光照无法反射到我们眼睛里。
这个函数的取值范围如下:
\[
\begin{align}
0\leq G(n,v,l,k)\leq 1
\end{align} \tag{33}
\] 我在代码中使用的是PBRT上提供的G项,不过我更推荐用\(G_{Schlick\text{-}GGX}\)来计算G项的值,计算量小。
Fresnel Term
菲涅尔函数会根据我们看向的角度不同,以及物体的折射率,得出总共反射的能量占比多大:

对于电介质,我们以垂直表面的方向去看,反射的能量并不是很多,而越是以掠射角去看向表面,反射的能量占比就越大:
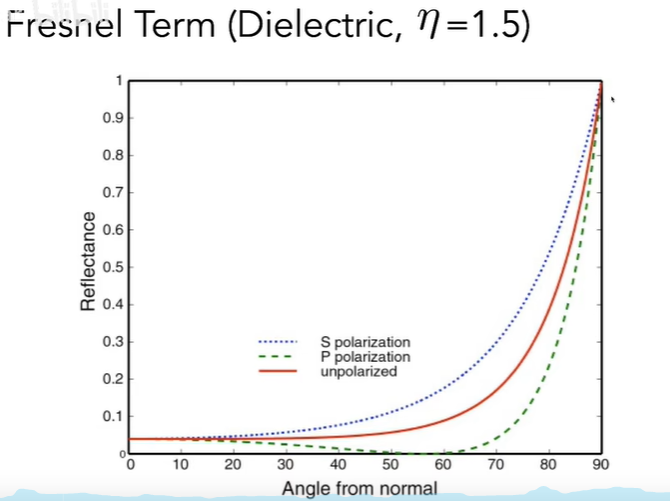
对于导体来说,因为其基础反射率很大,就算是以垂直表面的方向去看它,反射的能量占比也很大:
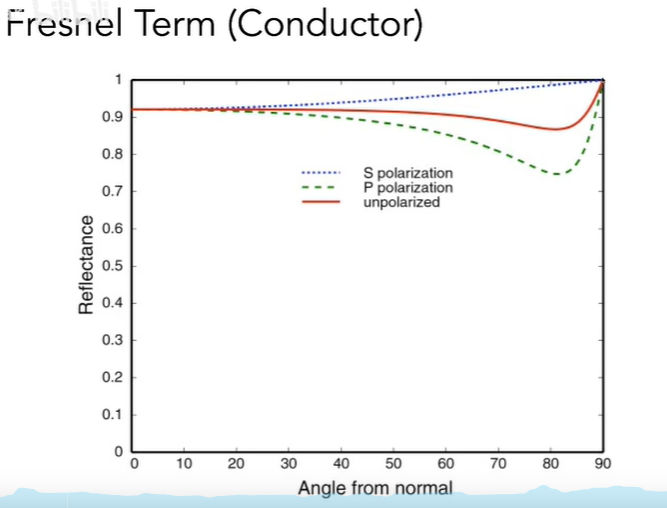
菲涅尔公式本身也比较复杂,它利用了光传输介质的折射率计算出平行偏振光和垂直偏振光,然后取各自平方的1/2加起来得出Fresnel值,这种方式计算出的Fresnel值很正确,但是计算量有点大:

我在代码中有实现这样算Fresnel项的函数,但是考虑到计算量的问题,我还是换了一个更加通用且计算量更小的计算方法:
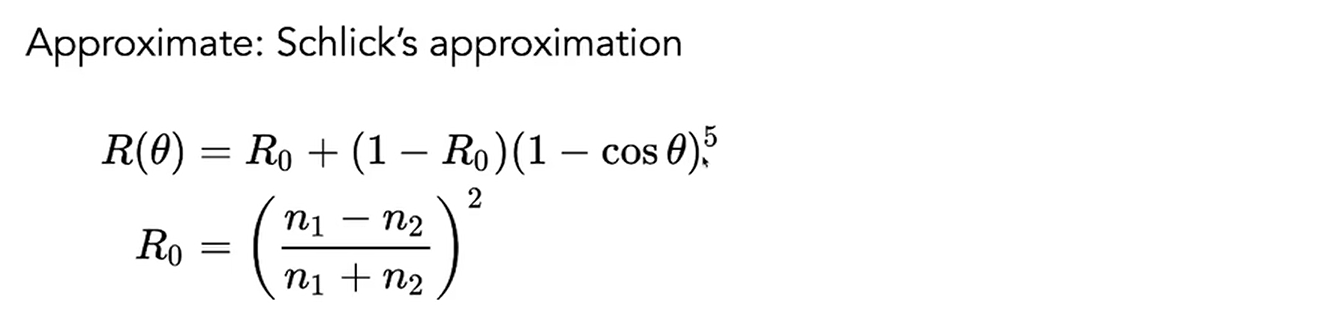
其中R_0是物质的基础反射率,电介质会很小,基本上取它们平均值0.04就行,而金属导体会很大,差异也很大,需要准确定义,还可以通过光传输介质来计算R_0。cosθ的两个参数是我们看向的方向和半程向量。
其取值范围如下:
\[
\begin{align}
0\leq F(v,h,ior,F_0)\leq 1
\end{align} \tag{34}
\]
BRDF效果图
在计算采样方向的pdf时需要注意,我们需要综合考虑漫反射和镜面反射的pdf值,然后加起来,这是用Fresnel项来控制的:
1
2
3double D = NDF(roughness, H, N);
Vector3f F = Fresnel_Schlick(H, wo, ior);
pdf.pdfValue = (F.x * D * dotProduct(H,N) / (4.0 * dotProduct(H, pdf.reflectDir))) + (1 - F.x) * dotProduct(pdf.reflectDir, N) / M_PI;4.0 * dotProduct(H, pdf.reflectDir)这个分母怎么来的可以看我这篇文章。
但是这里按理来说,应该要考虑以漫反射cos weight PDF生成采样方向wi的情况,但是我没写这部分,不过感觉效果好像也挺不错的哈哈:

这只兔子就是BRDF材质渲染出来的结果,代码就不贴了,这篇文章实在太长了。
BSDF
前面说了BSDF是有BRDF和BTDF组合而成:

\[
\begin{align}
f_r(i,o,n)=\frac{F(i,h_r)G(i,o,h_r)D(h_r)}{4|i\cdot n||o\cdot n|}
\end{align} \tag{35}
\] \[
\begin{align}
f_t(i,o,n)=\frac{|i\cdot h_t||o\cdot h_t|}{|i\cdot n||o\cdot n|}
\frac{\eta_{o}^{2}(1-F(i,h_t))G(i,o,h_t)D(h_t)}{(\eta_i(i\cdot
h_t)+\eta_o(o\cdot h_t))^2}
\end{align} \tag{36}
\]
BRDF跟上面SpecularBRDF差不多,这里的校正因子需要取绝对值。我们现在主要看下BTDF,这里的T是透射的意思。
i为视角方向,o为采样方向,这和上面BRDF是反着来的,需要注意一下,因为图例是来自论文,我没有做修改:
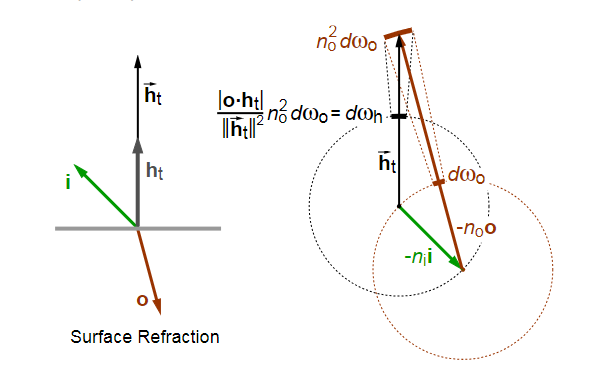
向量i,o,h_t都是归一化的向量,h_t是视角方向和透射采样方向的半程向量,h_r则是视角方向和反射采样方向的半程向量:
\[
\begin{align}
& h_r=\text{normalize}(i+o) \\
& h_t=\text{normalize}(-\eta_ii-\eta_oo)
\end{align} \tag{37}
\] \(\eta_i\)是图例中上方光传输介质的折射率,假设为空气,则\(\eta_i\)为1.0。
\(\eta_o\)是图例中下方光传输介质的折射率,假设为玻璃,则\(\eta_o\)为1.5。
如果光线是从玻璃内部逃逸出来,则这个过程是相反的。
接着看这个\(\eta_o^2\text{d}w_o\)怎么来的:
假设\(-\eta_oo\)对应的立体角为\(c*\text{d}w_o\),则有以下等式:
\[
\begin{align}
& \frac{c*\text{d}w_o}{||-\eta_o*o||^2}=\text{d}w_o \\
& c=\eta_o^2
\end{align} \tag{38}
\] pdf_h转换到pdf_o的等式为:
\[
\begin{align}
p_{o}(\theta,\phi)=p_{h}(\theta,\phi)\cdot\lVert\frac{\partial
w_{h}}{\partial w_{o}}\rVert \\
\end{align} \tag{39}
\] 后面那个是雅克比行列式,另外论文说这个\(\vec
{h_t}\)的定义变得模糊了,直接给出了这个行列式的公式,这里就不再推导了,我也是直接用的这个公式:
\[
\begin{align}
\lVert\frac{\partial w_{h}}{\partial w_{o}}\rVert=
\frac{\eta_o^2|o\cdot h_t|}{||\vec {h_t}||^2}=
\frac{\eta_o^2|o\cdot h_t|}{(\eta_i(i\cdot h_t)+\eta_o(o\cdot h_t))^2}
\end{align} \tag{40}
\]
最后需要注意一点的是,Fresnel_Schlick处理不了光线由玻璃向空气Trace的情况,我们这里还是得通过折射率计算出平行偏振光和垂直偏振光,然后得出准确的Fresnel项,这部分代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26double G, D;
Vector3f F;
Vector3f h = pdf.halfVec;
double etai = 1, etao = ior;//空气默认为1
if (isOutside == false)
std::swap(etai, etao);
F = Fresnel(-wo, h, isOutside);
//Trowbridge–Reitz GGx的几何项
G = G1G2(roughness, wo, wi, h);
//Trowbridge–Reitz GGx的法线分布项
D = NDF(roughness, h, N);
if (pdf.isReflect == true) {
// brdf
double divisor = 4 * std::abs(dotProduct(N, wo)) * std::abs(dotProduct(N, wi));
if (divisor < EPSILON) return {};
return F * G * D / divisor;
}
else {
// btdf
double prefixEntry = std::abs(dotProduct(wo, h)) * std::abs(dotProduct(wi, h)) / (std::abs(dotProduct(wo, N)) * std::abs(dotProduct(wi, N)));
double divisor1 = etai * dotProduct(wo, h) + etao * dotProduct(wi, h);
double divisor2 = divisor1 * divisor1;
if (divisor2 < EPSILON) return {};
return (prefixEntry * etao * etao * (Vector3f(1.0f) - F) * G * D) / divisor2;
}
return {};brdf+btdf,pdf也是一样,但是结果并不正确,模型最外圈会出现白色的圈,经过debug发现白圈是因为在掠射角下btdf的pdf小,而btdf过大导致的。所以我认为这里公式上虽然写的是brdf+btdf,但是实际处理还是得分开。反射的半程向量其实和透射的半程向量是一致的,所以我们只需要计算一次即可。
BSDF效果图
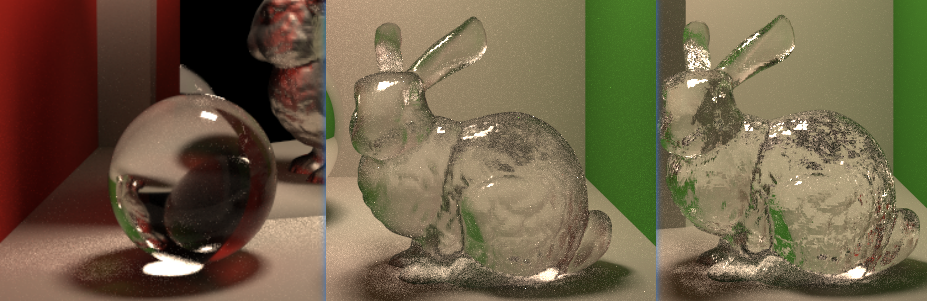
两边是Roughness为0.08的情况,中间是0.28。
Multiple Importance Sampling
多重重要性采样的目的是用来降低噪声的,我们知道渲染方程由Li,BRDF组成,而当我们进行采样时,我们可以选择其中一种pdf,并用蒙特卡洛积分求出积分值。但是现在有一个问题是,有时候我们需要BRDF进行采样而有时候又需要直接光采样,这就有问题了,看下面例子(这个多重重要性的场景是我自己搭建的):
16spp BRDF采样:

16spp 直接光采样:

可以看到只用直接光采样,或者只用BRDF采样,其效果都不行,但是它们却又能互补。在完全镜面的地方,直接光对大面积光源的采样效果非常差,而在比较粗糙的地方BRDF对小面积光源的采样效果也不好。而结合它们就可以取长补短,MIS正是解决这样的问题,它可以使用多种采样策略,然后根据一定权重将它组合起来:
假设这里有一个积分形如\(\int
f(x)g(x)\text{d}x\)我们可以用下面公式算得该积分的值:
\[
\begin{align}
\int
f(x)g(x)\text{d}x\approx\frac{1}{n_f}\sum_{i=1}^{n_f}\frac{f(X_i)g(X_i)w_f(X_i)}{p_f(X_i)}+
\frac{1}{n_g}\sum_{j=1}^{n_g}\frac{f(Y_j)g(Y_j)w_g(Y_j)}{p_g(Y_j)}
\end{align} \tag{41}
\]
其中w_f和w_g就是权重函数,由Power Heuristic公式所得:
\[
\begin{align}
w_s(x)=\frac{(n_sp_s(x))^\beta}{\sum_{i}(n_ip_i(x))^\beta}
\end{align} \tag{42}
\]
其中n_s为p_s采样策略的采样次数,n_i为p_i采样策略的采样次数,我们在代码使用的蒙特卡洛积分都是采样一次,所以它们都是1。而p(x)为各自采样策略的概率密度函数。β硬编码为2即可(更多内容请参考pbrt)。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72double PowerHeuristic(double nf, double fPdf, double ng, double gPdf) const {
double f = nf * fPdf, g = ng * gPdf;
return (f * f) / (f * f + g * g);
}
Vector3f Scene::mis_directLight(Intersection intersection,Vector3f wo,Intersection L_dir_Inter,double pdf_light, int depth) const
{
Vector3f Le(0.0);
MaterialType interType = intersection.m->getType();
//1. 直接对光源采样
//起始点
Vector3f p = intersection.coords;
//光源位置点
Vector3f x = L_dir_Inter.coords;
//光源方向,直接光的入射方向
Vector3f w_Li = (x - p).normalized();
Ray p_2_light_ray(p, w_Li);
...
Intersection p_2_light_inter = intersect(p_2_light_ray);
//击中的是光源 且 起始点的材质不是镜面或者透明。
if (p_2_light_inter.happened && p_2_light_inter.m->hasEmission() && interType != MIRROR && interType != TRANSPARENT)
{
Pdf pdf;
pdf.halfVec = normalize(wo + w_Li);
double light_solidAngle_pdf = pdf_light;
intersection.m->mis_getpdf(interType, intersection.normal,wo, w_Li,pdf);
double brdf_solidAngle_pdf = pdf.pdfValue;
Vector3f f_r = intersection.m->eval(wo, w_Li, intersection.normal, intersection.isOutside, pdf);
double weight = PowerHeuristic(1.0, light_solidAngle_pdf, 1.0, brdf_solidAngle_pdf);
...
Le = L_dir_Inter.emit * f_r * std::fmax(dotProduct(w_Li, intersection.normal),0.0) / light_solidAngle_pdf * weight;
}
//2.brdf对光源采样
Pdf pdf;
Vector3f wi = (intersection.m->sample(wo, intersection.normal, intersection.isOutside, pdf)).normalized();
...
Vector3f bxdf = intersection.m->eval(wo, wi, intersection.normal, intersection.isOutside, pdf);
Ray L_brdf_Ray = Ray(p, wi);
...
Intersection L_brdf_Inter = intersect(L_brdf_Ray);
//击中的是光源 且 起始点的材质不是镜面或者透明。
if (L_brdf_Inter.happened && L_brdf_Inter.m->hasEmission() && interType != MIRROR && interType != TRANSPARENT)
{
//起始点
Vector3f newP = intersection.coords;
//光源位置点
Vector3f newX = L_brdf_Inter.coords;
double lightDistance = (newX - newP).norm();
double lightDistance2 = lightDistance * lightDistance;
double newPdf_light = 0.0;
//面光源
if (dynamic_cast<Sphere*>(L_brdf_Inter.obj) == nullptr) {
//面光源是两个三角形组成 * 2
newPdf_light = lightDistance2 / L_brdf_Inter.obj->getArea() * 2 * std::fmax(dotProduct(-wi, L_brdf_Inter.normal), 0.0);
}
//球光源
else {
Intersection tmp;
tmp.tcoords = intersection.coords;
//只用拿到pdf就行
L_brdf_Inter.obj->Sample(tmp, newPdf_light);
}
double light_solidAngle_pdf = newPdf_light;
double brdf_solidAngle_pdf = pdf.pdfValue;
double weight = PowerHeuristic(1.0, brdf_solidAngle_pdf, 1.0, light_solidAngle_pdf);
Le += L_brdf_Inter.m->getEmission() * bxdf * std::fmax(dotProduct(wi, intersection.normal), 0.0) / brdf_solidAngle_pdf * weight;
}
//镜面和透明物质单独处理,这是直接光。
...
return Le;
}

## Sampling a Sphere Object
另外因为光源是个球,我们需要对球进行采样,其过程如下(下面部分内容来源于RayTracingTheRestOfYourLife):
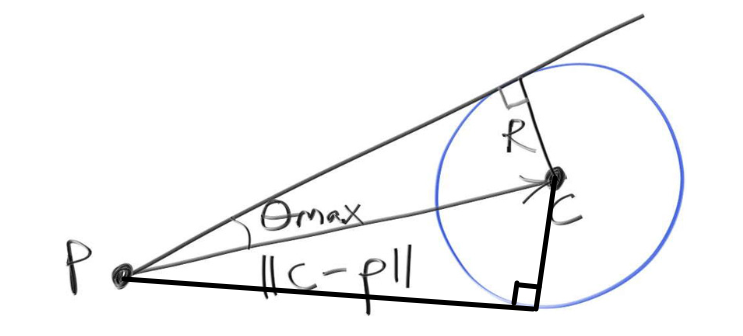
对于一个着色点P,我们要在正对着它的球光源上均匀的取一个采样点,所以我们有以下等式:
\[
\begin{align}
1=\int_{0}^{2\pi}\int_{0}^{\theta_{max}}f(\theta)\sin\theta\text{d}\theta\text{d}\phi
\end{align} \tag{43}
\]
因为是均匀采样,这里f(θ)其实是一个常数,我们尚且将其设为C,然后分别求其边缘概率密度函数:
\[
\begin{align}
& p(\theta)=\int_{0}^{2\pi}C\sin\theta\text{d}\phi \\
& p(\theta)=C2\pi\sin\theta \\
& p(\phi)=\int_{0}^{\theta_{max}}C\sin\theta\text{d}\theta \\
& p(\phi)=C(1-\cos\theta_{max})
\end{align} \tag{44}
\] 再分别求其累积分布函数:
\[
\begin{align}
& P(\theta)=\int_{0}^{\theta}C2\pi\sin\theta\text{d}\theta \\
& P(\theta)=C2\pi(1-\cos\theta) \\
& P(\phi)=\int_{0}^{\phi}C(1-\cos\theta_{max})\text{d}\phi \\
& P(\phi)=\phi*C(1-\cos\theta_{max})
\end{align} \tag{45}
\]
根据CDF的性质,在θ等于θ_max时,有以下等式:
\[
\begin{align}
& 1=\int_{0}^{\theta_{max}}C2\pi\sin\theta\text{d}\theta \\
& 1=C2\pi(1-\cos\theta_{max}) \\
& C=\frac{1}{2\pi(1-\cos\theta_{max})}
\end{align} \tag{46}
\] 由图57可知,\(\sin(\theta_{max})\)为:
\[
\begin{align}
& \sin(\theta_{max})=\frac{R}{\text{length}(c-p)} \\
& \cos(\theta_{max})=\sqrt{1-\frac{R^2}{\text{length}^2(c-p)}}
\end{align} \tag{47}
\] 则:
\[
\begin{align}
&
P(\theta)=\frac{1-cos\theta}{1-\sqrt{1-\frac{R^2}{\text{length}^2(c-p)}}}
\\
& P(\phi)=\frac{\phi}{2\pi}
\end{align} \tag{48}
\]
我们均匀的从U[0,1]中取出两个随机数X_1,X_2则我们要的采样方向θ和φ为:
\[
\begin{align}
& \cos\theta=1+X_1(\cos(\theta_{max})-1) \\
& \phi=2\pi X_2 \\
& z=\cos\theta=1+X_1(\cos(\theta_{max})-1) \\
& x=\cos\phi\sin\theta=\cos(2\pi*X_2)*\sqrt{1-\cos^2\theta} \\
& y=\sin\phi\sin\theta=sin(2\pi*X_2)*\sqrt{1-\cos^2\theta}
\end{align} \tag{49}
\] 我们现在来求球光源投影到着色点P的立体角:
\[
\begin{align}
&
\text{solid-angle}=\int_{0}^{2\pi}\int_{0}^{\theta_{max}}\sin\theta\text{d}\theta\text{d}\phi
\\
& \text{solid-angle}=2\pi*(1-\cos(\theta_{max}))
\end{align} \tag{50}
\] 则pdf为\(\frac{1}{solid-angle}\),代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void Sample(Intersection &pos, double &pdf){
//对球进行采样
double cos_theta_max = sqrt(1- radius2/(center - pos.tcoords).norm());
double phi = 2.0 * M_PI * get_random_double();
double z = 1 + get_random_double() * (cos_theta_max - 1);
Vector3f dir(sqrt(1 - z * z) * std::cos(phi), sqrt(1 - z * z) * std::sin(phi), z);
dir = toWorld(dir, normalize(pos.tcoords - center));
pos.coords = center + radius * dir;
pos.normal = dir;
pos.emit = m->getEmission();
double solid_angle = 2 * M_PI * (1 - cos_theta_max);
pdf = 1.0 / solid_angle;
}